คุณเคยเจอคนมาเสนอขายประกันชีวิตมั๊ยครับ? ผมรับรองว่าคุณต้องเคยเจอแน่นอน (และคงไม่ต่ำกว่า 1 ครั้งในรอบ 1 ปีด้วย!! ) แต่สิ่งที่พวกเราเจอส่วนใหญ่ จะถูกนำเสนอว่าแผนประกันแบบโน้นแบบนี้ดีมากๆ ได้ผลตอบแทนหลายเท่าของเงินลงทุนของเรา (เช่น ผลตอบแทน 200%) แต่มันจะจริงแค่ไหนน้า????
ปล. ตอนนี้เป็นตอนที่ 2 ต่อจากการปูพื้นฐานด้านการเงิน ในตอนที่แล้ว ใครยังไม่ได้อ่าน สามารถไปอ่านได้เลยที่นี่ครับ
จากประกันชีวิต ทำไมมันเยอะจัง?
ถ้าเราเป็นคนที่ไม่ค่อยมีความรู้ด้านการเงิน คงจะตะลึงและคล้อยตามกับการนำเสนอของตัวแทน เพราะได้เงินตอบแทนกลับมามากกว่าเงินลงทุน ยังไงก็คุ้ม ได้เงินตั้ง 200-300% ดีกว่าเงินฝากประจำ หรือ เล่นหุ้นอีก แถมไม่เห็นมีอะไรน่าจะเสี่ยงตรงไหนเลย…
ถ้าเราลองมาคิดดีๆ เลข 200% ที่ประกันชีวิตชอบโฆษณามันคือ เงินคืนทั้งหมด เทียบกับจำนวนเอาประกัน ซึ่งไม่รู้จะเทียบกันทำไม เพราะไม่ใช่สิ่งที่เราจ่ายซักหน่อย สิ่งที่เราจ่ายไปจริงๆ มันมากกว่าจำนวนเงินเอาประกันตั้งเยอะ… (ลองบวกดูสิ)
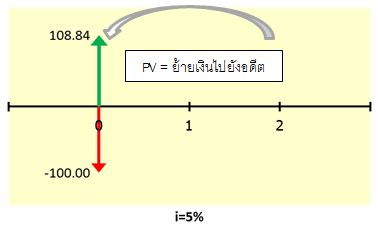
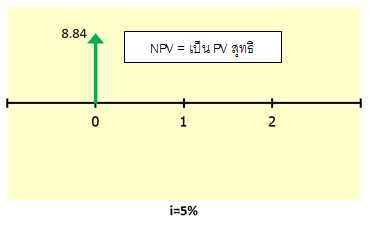
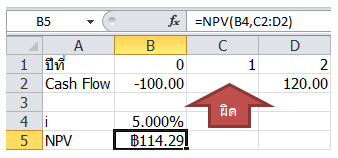
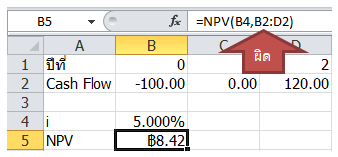
จากความรู้ที่ผ่านมา เราได้รู้ว่า การได้จำนวนเงินตอบแทนมากกว่าเงินลงทุนไม่จำเป็นจะต้องเป็นการลงทุนที่ดีนะครับ เช่น สมมติผมลงทุนด้วยเงิน 1 แสนบาท แล้วมีแผนประกัน 2 แผน อันแรก เรียกว่าแผน A บอกว่าได้เงินตอบแทนรวมทั้งหมด 3 แสนบาท ส่วนแผน B ได้เงินตอบแทนรวมทั้งหมด 2 แสนบาท แบบนี้ แผน A ไม่จำเป็นต้องคุ้มกว่าแผน B นะครับ ทั้งนี้เพราะ Effect เรื่อง Time Value of Money นั่นเอง
ดังนั้นเราจะใช้แนวทางการวิเคราะห์ Project ด้วยวิธี IRR ในการตัดสินใจเลือกแผนประกันชีวิตกันครับ โดยเราจะหา IRR ของแผนแต่ละอัน แล้วหาอันที่ IRR สูงสุด นั่นเอง (แล้วค่อยเทียบกับค่า Required Return ในใจเราอีกที)
แผน A
มีลักษณะดังนี้
- ชำระเบี้ยประกัน 4 ปี คุ้มครอง 10 ปี
- ทุกสิ้นปีกรมธรรม์ที่ 1-3 รับเงินจ่ายคืนปีละ 4% ของทุนประกัน
- ทุกสิ้นปีกรมธรรม์ที่ 4-6 รับเงินจ่ายคืนปีละ 5% ของทุนประกัน
- ทุกสิ้นปีกรมธรรม์ที่ 7-9 รับเงินจ่ายคืนปีละ 6% ของทุนประกัน
- รับเงินครบกำหนดสัญญา 180% ของทุนประกัน ณ สิ้นปีกรมธรรม์ที่ 10
ผมขอไม่พูดถึงเรื่องความคุ้มครองแล้วกันนะครับ Assume ว่าเราจะยังมีชีวิตอยู่จนจบแผนประกัน
ที่นี้สิ่งที่เรายังไม่รู้คือ เราต้องชำระเบี้ยประกันปีละเท่าไหร่ ซึ่งอันนี้ต้องให้เจ้าหน้าที่ตัวแทนประกันที่เป็นคนบอกราคามาให้ครับ ว่าค่าเบี้ยคุณต้องจ่ายปีละเท่าไหร่ เพราะมันขึ้นอยู่กับความเสี่ยง เช่น เพศ และอายุของแต่ละคน
สมมติว่าผมจะทำประกันโดยจำนวนเอาประกันเป็น 100,000 ทางตัวแทนบอกราคาให้ผมจ่ายเบี้ยประกันปีละ 51,000 บาท ผมสามารถทำเป็นตาราง Excel และคิด IRR ได้ดังนี้

เงินรับ : จะเห็นว่าผมพยายามใส่สูตรเป็น Cell Reference ให้ Excel คำนวณให้มากที่สุดเท่าที่จะทำได้ โดยไม่คำนวณด้วยมือ เช่น ถ้าเรารู้ว่าเงินคืนคิดเป็น % จากทุนประกัน เราก็ควรผูกสูตรตามนั้น เพื่อที่จะลดความผิดพลาด และให้เราเปลี่ยนค่าเล่นได้ในอนาคต
เงินจ่าย : อย่าลืมว่าเราจ่ายค่าเบี้ย 4 ปี แปลว่าเราจะจ่ายที่ปีที่ 0,1,2,3 เท่านั้น ไม่ได้จ่ายตอนสิ้นปีที่ 4 นะครับ
คุณสามารถใส่ Cash Flow ที่เป็นการจ่ายให้เป็นลบ แล้ว Cash Flow สุทธิให้เอารับ+จ่าย หรือว่าจะให้ Cash Flow ทั้งรับและจ่ายเป็นบวก แล้ว Cash Flow สุทธิ เอา รับ – จ่ายก็ได้ ไม่ว่ากัน ถูกทั้งคู่
ที่สำคัญคือ IRR จะต้องคิดจาก Cash Flow สุทธิเท่านั้น และต้องรวมปีที่ 0 ด้วย จึงต้องเขียนว่า =IRR(B9:L9) ซึ่งแผนนี้จะออกมาได้ 1.3% เท่านั้น
แผน A + ลดหย่อนภาษี
ที่นี้หลายคนคงเริ่มสงสัยเรื่องการลดหย่อนภาษีจากเบี้ยประกันชีวิต ซึ่ง % ที่เอาไปลดหย่อนได้ ขึ้นอยู่กับฐานภาษีของแต่ละคน ไม่เท่ากัน โดยที่ฐานภาษีสำหรับปีภาษี 2556 และ 2557 เป็นแบบขั้นบันไดดังนี้
ช่วงรายได้สุทธิ => ภาษี
- 1 – 150,000 => 0%
- 150,001 – 300,000 => 5%
- 300,001 – 500,000 => 10%
- 500,001 – 750,000 => 15%
- 750,001 – 1,000,000 => 20%
- 1,000,001 – 2,000,000 => 25%
- 2,000,001 – 4,000,000 => 30%
- 4,000,001 บาทขึ้นไป => 35%
ถ้าถามว่าผลประโยชน์จากการลดหย่อนภาษีมันจะนำมาคำนวณในนี้ยังไง ผมขอยกตัวอย่างแบบนี้ครับ สมมติว่ารายได้สุทธิของคุณหักค่าลดหย่อนทุกอย่างแล้ว อยู่ที่ปีละ 250,000 บาท แปลว่า
ถ้าไม่มีประกันชีวิต คุณต้องจ่ายภาษี = 5% * (250000-150000) = 5000 บาท/ปี (ถ้ารายได้ไม่เปลี่ยน)
ถ้าคุณจ่ายเบี้ยประกัน 51,000 บาท แปลว่าคุณจะมีรายได้สุทธิอยู่ที่ =250,000-51,000= 199,000 บาท แปลว่าคุณต้องจ่ายภาษี = 5% * (199000-150000) = 2450 บาท/ปี (ถ้ารายได้ไม่เปลี่ยน) นั่นคือ ประกันชีวิต ช่วยลดรายจ่ายของคุณไปปีละ 5000-2450 = 2550 บาท/ปี (ไม่ใช่ลดไป 51000 นะครับ!! อย่าเข้าใจผิด)
หรือจะคิดง่ายๆ ก็คือเอาอัตราภาษี * เบี้ยประกันก็ได้ (ถ้าอยู่ช่วงเดียวก็ง่ายหน่อย) เช่น =5%*51000 = 2550 บาท เช่นกัน
แต่ถ้าจะคิดเผื่อเรื่องของเวลาด้วย ถ้าคุณจ่ายเบี้ยประกันต้นปีนี้ กว่าคุณจะได้เงินภาษีคืนก็คือในต้นปีหน้า ดังนั้นคุณอาจต้องเลื่อนผลประโยชน์จากภาษีไปอีกปีนึง แต่ถ้าคุณจ่ายเบี้ยประกันปลายปี อาจไม่จำเป็นต้องเลื่อนก็ได้ เพราะเวลาไม่ห่างมากนัก
สรุปแล้ว สมมติผมจ่ายประกันต้นปี ผมจึงควรเลื่อนผลประโยชน์ภาษีออกไปปีถัดไป เราจึงปรับตารางให้เป็นดังนี้

จะเห็นว่า IRR มีค่าเพิ่มขึ้นมาเยอะเลย อันนี้แหละน่าจะเป็นประโยชน์ของประกันชีวิต ในแง่ของการเงิน ซึ่งอาจจะเห็นผลน้อยถ้าหากว่ามีฐานภาษีที่น้อย แต่ประโยชน์จะเยอะขึ้นมาก คุณต้องจ่ายภาษีเยอะๆ เช่น 30% เป็นต้น
เป็นยังไงบ้างครับ ผมหวังว่าเพื่อนๆ คงมีความรู้พอที่จะวิเคราะห์แผนประกันกันได้เองแล้วนะครับ ใครเจอแผนไหนดีๆ ได้ผลตอบแทนสูงๆ ก็บอกมาได้นะครับ เผื่อประกันเดิมที่ผมมีจะจ่ายหมดแล้ว จะได้ซื้อตัวใหม่ไว้ลดหย่อนภาษีอีกครับ อิอิ
ตอนหน้า เดี๋ยวเรามาต่อเรื่องการผ่อนเงินกู้ เช่น กู้บ้าน ซึ่งเราจะมาใช้ฟังก์ชั่น PMT กันครับ