จากที่ผมได้ Post ใน Facebook ไปว่าจะสอนเรื่องการวิเคราะห์แผนประกันชีวิตด้ว
สารบัญ
เงิน 100 บาทในวันนี้ กับเงิน 100 บาทใน 10 ปีข้างหน้า ไม่ได้มีมูลค่าเท่ากัน

ถ้าให้คิดเล่นๆ ผมให้คุณเลือกเอาว่าคุณจะเอา 100 บาทวันนี้เลย หรือต้องรอ 10 ปี เพื่อเอาเงิน 100 บาท? ถ้าคุณเป็นคนปกติทั่วไปน่าจะต้องเลือกเอา 100 บาทในวันนี้ใช่มั๊ยล่ะครับ
นั่นแปลว่า ถ้าจำนวนเงินเท่ากัน เงินในปัจจุบัน (Present Value :PV) จะมีค่ากับคุณมากกว่าเงินในอนาคต (Future Value :FV) หรือในทางกลับกัน จะบอกได้ว่า เงินในอนาคตจะถูกลดทอนมูลค่าลง (Discount) เมื่อนำมาเทียบกับค่าของเงินในปัจจุบันนั่นเอง เราเรียกปรากฏการณ์นี้ว่า Time Value of Money ครับ
คำถามจะเริ่มยากขึ้น ถ้าจำนวนเงินไม่เท่ากัน เช่น คุณจะเอา 100 บาทวันนี้เลย หรือต้องรอ 10 ปี เพื่อเอาเงิน 200 บาท แบบนี้เริ่มคิดมากขึ้นแล้วใช่มั๊ยครับ? แปลว่า คุณต้องมีวิธีคิดแล้วว่าถ้าต้องรอขนาดนั้น ต้องได้เท่าไหร่ถึงจะคุ้ม
เงินในอนาคตจะถูก Discount ลงไปเท่าไหร่?
ถ้าผมจะบอกว่า “ผมบอกไม่ได้ มันแล้วแต่คุณ” ล่ะครับ… ผมไม่ได้กวนนะ ทั้งนี้เพราะว่า การที่เงินแต่ละปีมีค่าไม่เท่ากัน เป็นเพราะเกิดจาก “ผลตอบแทนที่ต้องการหรือคาดหวังจากการลงทุน” (Required rate of return) ซึ่งเป็นสิ่งที่ขึ้นอยู่กับแต่ละบุคคลนั่นเอง
ซึ่งผลตอบแทนคาดหวังของการลงทุน นั้นขึ้นอยู่กับหลายๆ ปัจจัย แต่หลักๆ ก็จะพิจารณาเรื่องความเสี่ยง และ ค่าเสียโอกาส ซึ่งหมายถึง ต้องพิจารณาทางเลือกที่ดีที่สุดที่เรายอมทิ้งไปเพื่อแลกกับสิ่งที่เรากำลังตัดสินใจอยู่
มันจึงมีชื่อเรียกหลายชื่อ ทั้ง Required rate of return, Interest Rate, Discount Rate, Hurdle Rate ทุกอันคือสิ่งเดียวกัน ยกตัวอย่างเช่น ถ้าเราต้องลงทุนในโปรเจคอะไรซักอย่างที่มีความเสี่ยงสูง เราคงต้องอยากได้ผลตอบแทนสูงๆ มาชดเชยความเสี่ยงนั้นใช่มั๊ยครับ? นั่นแหละคือ Required rate of return ของเรา ซึ่งแต่ละคนไม่จำเป็นต้องการเท่ากัน
ใครมีทางเลือกในชีวิตเยอะ อาจต้องการ Required rate of return สูงกว่า เพราะถ้าโปรเจคนี้ผลตอบแทนไม่ดีพอ เค้าก็สามารถไปลงทุนอย่างอื่นที่ผลตอบแทนดีกว่าได้ ต่างจากคนที่ไม่ค่อยมีทางเลือก ซึ่งอาจมีแค่เงินฝากประจำเป็นทางเลือกสำรอง ซึ่งเป็นทางเลือกที่ผลตอบแทนค่อนข้างต่ำ
การวิเคราะห์เรื่อง Time Value of Money ด้วยการวาดรูป
เวลามีเรื่องของ Time Value of Money ขึ้นมาเมือไหร่ สิ่งแรกที่ผมอยากจะให้เราคิดเลย ก็คือ การคิด หรือวาดรูปออกมาเป็นภาพ (เรียกว่า Cash flow Diagram) ซึ่งการคิดเป็นภาพเป็นพื้นฐานที่ดีในการที่เราจะแปลงภาพเหล่านี้เป็นตารางใน Excel ภายหลัง
ซึ่งเราจะวาดภาพที่มีองค์ประกอบดังนี้
- เส้นแกนนอนเป็นเวลา โดยแบ่งออกเป็นแต่ละช่วง แล้วแต่โจทย์ว่ามีการคิดดอกเบี้ยช่วงหนึ่งๆ นานเท่าไหร่
- เราสามารถระบุจุดของเวลาได้ 2 แบบ คือ Begin of Period กับ End of Period แต่ปกติแล้วจะนิยมเขียนเป็น End of Period มากกว่า
- เวลาที่ Period 0 ที่เป็นจุดเริ่มต้น คือเวลาปัจจุบันที่เริ่มมี Action อะไรบางอย่าง เช่น การลงทุนเงินของเรา เป็นต้น เช่น เริ่ม 1 พค. 57
- เมื่อเวลาผ่านไป 1 Period (เช่น 1 ปี) ก็จะหลายเป็น Period ที่ 1 คือวันที่ 1 พค. 58 เป็นต้น
- ลูกศรชี้ขึ้นแทนเงินที่ได้รับ (เงินเป็น +)
- ลูกศรชี้ลงแทนเงินที่จ่ายออกไป (เงินเป็น -)
- มีการระบุผลตอบแทนที่คาดหวัง หรือ อัตราดอกเบี้ยที่จะใช้ในแต่ละช่วง ว่ามีค่าเท่าไหร่
ตัวอย่าง
ถ้าคุณลงทุน 100 บาท ใน Project A แล้วคาดว่าอีก 2 ปีข้างหน้าจะได้เงินคืนมา 120 บาท โดยมี Discount Rate ที่ 5% แบบนี้เราจะเขียนรูปได้ดังนี้

คำศัพท์พื้นฐานเกี่ยวกับสูตรทางการเงินของ Excel
- PV = Present Value คือ หามูลค่าเงินในปัจจุบัน
- FV = Future Value คือ หามูลค่าเงินในอนาคต
- Rate = อัตราดอกเบี้ยคาดหวัง หรือ Discount Rate
- Nper = จำนวน Period ที่จะทำการเคลื่อนย้าย Cash Flow
- PMT = การแบ่งเงินเพื่อผ่อนชำระเป็นงวด งวดละเท่าๆ กัน (เช่น การคำนวณเงินกู้ซื้อบ้าน) ถ้าไม่ได้มีการผ่อนก็ใส่เลข 0 ไป
PV
ดังนั้น หากเราอยากจะรู้ว่าเงิน 120 บาทใน 2 ปีข้างหน้า (Future Value) จะมีมูลค่าในปัจจุบัน (Present Value) เท่าไหร่? เราสามารถใช้ฟังก์ชั่น PV ใน Excel มาช่วยได้
- =PV(rate,nper,pmt,[fv],[type])
- =PV(5%,2,0,120) = -108.84
นั่นหมายถึงว่า เงิน 120 บาทใน 2 ปีข้างหน้า ถ้า Discount กลับมาที่เวลาปัจจุบันจะมีมูลค่า 108.84 บาท
ส่วนเครื่องหมายติดลบเพราะ Excel จะทำให้เครื่องหมายของ PV กับ FV ตรงข้ามกันให้โดยอัตโนมัติ ถ้าเราไม่อยากให้มันติดลบ ให้เราใส่ค่า FV เป็นติดลบไปก่อน มันจะได้กลายเป็นบวกตามปกติ ดังนี้
- =PV(5%,2,0,-120) = 108.84
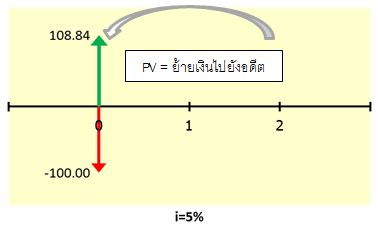
นั่นแปลว่าผลตอบแทนการลงทุนมีมูลค่า 108.84 บาท เทียบกับการลงทุน 100 บาท เมื่อนำมาหักลบกัน จะได้สิ่งที่เรียกว่า Net Present Value หรือ NPV ซึ่งก็เป็นอีกฟังก์ชั่นหนึ่งของ Excel เช่นกัน ซึ่งในที่นี้ NPV = 8.84 บาท ซึ่งถ้า NPV > 0 แปลว่าคุ้มค่า สรุป NPV คือเอา Cash Flow ทั้งหมด ย้ายมา ณ เวลาปัจจุบัน แล้วหา Cash flow สุทธิ
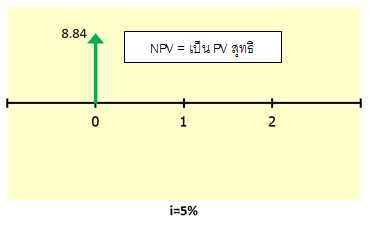
NPV ใน Excel
แต่ทว่าฟังก์ชั่น NPV ใน Excel ไม่ได้มีความหมายอย่างเดียวกับวิชา Finance ซะทีเดียว เพราะสิ่งที่มันทำ คือ เป็นการ ย้าย Cash flow สุทธิในอนาคตทุกตัวกลับมาที่ปัจจุบัน แต่มันยังไม่ได้หาค่าสุทธิกับ Cash flow ที่อยู่ Period ที่ 0 ให้
ทั้งนี้มีข้อควรระวัง 2 ข้อ คือ
- ปีไหนไม่มี Cash Flow จะต้องใส่เลข 0 ลงไปด้วย ห้ามปล่อยเป็นค่าว่าง ไม่งั้นมันจะคิดผิด
- วิธีการ input ค่าของฟังก์ชั่น NPV จะต้องเริ่มลากจาก Period ที่ 1 เป็นต้นไป ห้ามลากตั้งแต่ Period ที่ 0
ผิด เพราะลืมใส่ 0 ลงไปในปีที่ไม่มี Cash Flow
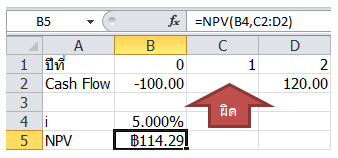
ผิด เพราะลากคลุม Cash Flow ปีที่ 0 ไปด้วย
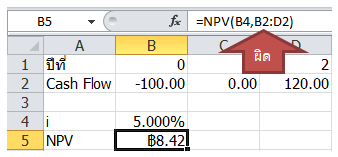
ถูกต้อง

จากนั้นค่อยเอาผลจากสูตร NPV มาสุทธิกับ Cash Flow ปีที่ 0 ภายหลัง ก็จะได้ NPV จริงๆ เป็น 8.84 นั่นเอง
FV
หากเราลองปรับค่าการลงทุนในปัจจุบัน ให้เป็นเงินในอนาคตบ้าง แบบนี้ก็ทำได้เช่นกัน โดยใช้สูตร FV ดังนี้
- =FV(rate,nper,pmt,[pv],[type])
- =FV(5%,2,0,100) = -110.25 บาท

ซึ่งการตีความผลลัพธ์จะได้ว่า มูลค่าเงินลงทุน น้อยกว่าผลตอบแทนที่ได้รับในเวลาเดียวกัน แปลว่าเป็นการลงทุนที่คุ้มเช่นกัน แต่เราจะไม่เรียกมันว่า NPV แล้ว เพราะไม่ใช่มูลค่าในปัจจุบัน
วิธีนี้ มักใช้กับคำถามที่ว่า เงินของฉันในตอนนี้ จะมีมูลค่าเท่าไหร่ในอีก xxx ปีข้างหน้า ซึ่งถ้า Discount rate เยอะๆ เพื่อนๆ จะตกใจในมูลค่าของมันเลยทีเดียว ดังคำกล่าวของไอน์สไตน์ที่ว่า พลังแห่งการคิดดอกเบี้ยทบต้น เป็นสิ่งที่ทรงพลังที่สุด เช่น ถ้าคุณมีเงิน 100 บาท แล้วไปหาแหล่งลงทุนที่ให้ผลตอบแทนได้ 10% ทุกปี ในอีก 60 ปีข้างหน้าเงินนี้จะมีมูลค่าถึง =FV(10%,60,0,-100) = 30,448.16 บาท เลยล่ะ!!
แล้วถ้าจะหาว่า interest rate เท่าไหร่ที่ทำให้คุ้มค่าพอดี
หลายคนคงเริ่มสงสัยแล้ว ว่า Discount Rate ที่เท่าไหร่ ที่จะทำให้การลงทุนนี้ “คุ้มค่าพอดี” มันก็คือ Discount Rate ที่ทำให้ NPV เป็น 0 พอดีนั่นเอง แต่เรามีคำศัพท์เรียกสิ่งนี้โดยเฉพาะว่า IRR หรือ Internal Rate of Return นั่นเอง ซึ่งเป็นสิ่งที่ Excel มีฟังก์ชั่นคำนวณให้โดยเฉพาะเช่นกัน
IRR
=IRR(values,guess)
ในช่อง Value ให้เราใส่ Range ที่เป็น Cash Flow สุทธิ ตั้งแต่ปีที่ 0 ถึงปีสุดท้ายเข้าไปเป็น Range
ทั้งนี้มีข้อควรระวัง 2 ข้อ คือ
- ปีไหนไม่มี Cash Flow จะต้องใส่เลข 0 ลงไปด้วย ห้ามปล่อยเป็นค่าว่าง ไม่งั้นมันจะคิดผิด
- วิธีการ input ค่าของฟังก์ชั่น IRR จะต้องเริ่มลากจาก Period ที่ 0 เป็นต้นไป ไม่เหมือน NPV
ผิด เพราะลืมใส่ 0 ลงไปในปีที่ไม่มี Cash Flow


สรุปเกณฑ์การตัดสินใจการลงทุน Project
คุณสามารถใช้เกณฑ์การตัดสินใจว่าจะลงทุนสิ่งที่เราสนใจ หรือ Project หรือไม่ อยู่ 2 แนวทาง คือ
- หาอัตราผลตอบแทนของ Project ด้วย IRR แล้วเทียบกับผลตอบแทนคาดหวัง IRR มากกว่าผลตอบแทนคาดหวังก็น่าลงทุน แต่ถ้ามีหลาย Project ที่ IRR มากกว่า แล้วมีเงินลงทุนจำกัด ก็ให้เลือก Project ที่ IRR สูงสุด
- ใช้ผลตอบแทนคาดหวัง ในการ Discount มูลค่าเงินที่จะได้ในอนาคต แล้วหาค่า NPV ถ้ามากกว่า 0 ก็น่าลงทุน
เอาล่ะครับ เมื่อเรามีความรู้พื้นฐานทางด้านการเงินแล้ว ตอนต่อไปเราจะมาวิเคราะห์แผนประกันชีวิตกันจริงๆ แล้วล่ะ



Leave a Reply