หลายๆ คนคงเคยเห็นสูตรที่เอาไว้แก่สมการกำลังสองเพื่อหาค่า x
โดยที่หากเราจัดสมการให้อยู่ในรูปแบบ
y=ax^2+bx+c
แล้วถ้าเราจัดเพื่อแก่สมการหาค่า x ที่ทำให้ y =0 เราจะได้ว่า
x=\frac{-b±\sqrt{(b^2-4ac)}}{2a}ซึ่งหลายๆ คนมองเหมือนว่ามันเป็นสูตรวิเศษที่เอาไว้ท่องจำแล้วแทนค่าอย่างเดียว แต่จริงๆ แล้วมันมีความหมายและที่มาที่ไปที่ควรจะรู้ไว้ด้วยนะ
ก่อนอื่นต้องบอกว่า การจะแก้สมการได้นั้นมี 2 วิธีใหญ่ๆ คือ
- แยกตัวประกอบ
- ใช้สูตร
วิธีแยกตัวประกอบ
โดยหลักการถ้าอะไรที่แยกตัวประกอบได้เลย มันก็สามารถคิดเลขในใจได้ง่าย
สมมติโจทย์ คือ
2x^2+10x-12 = 0
แบบนี้เราควรทำให้อยู่ในรูปแบบง่ายสุดก่อน เช่น หาร 2 ทั้งหมด ก็จะได้ว่า
x^2+5x-6 = 0
จากนั้นก็ดูว่า เลข 2 ตัวอะไรเอ่ย? คูณกันได้ -6 แต่บวกกันได้ 5
- ลองแยกตัวประกอบ -6 ก็ จะมี -1×6, 1x-6 ไม่ก็ -2×3, 2x-3
- ดังนั้นในเคสนี้ต้องเลือก -1 กับ 6 อ่ะนะ
ทำให้แยกได้แบบนี้
(x-1)(x+6) = 0นั่นคือ การที่มันจะเป็น 0 ได้ แสดงว่าแต่ละก้อนเป็น 0 นั่นคือ
- x-1 =0 ทำให้รู้ว่า x= 1
- x+6 =0 ทำให้รู้ว่า x= -6
วิธีใช้สูตร
ถ้าเขียนสูตร Excel หรือเขียน Code ก็จะใช้วิธีที่สองง่ายกว่ามานั่งแยกตัวประกอบ (เพราะมันคำนวณออกมาได้เลย)
x=\frac{-b±\sqrt{(b^2-4ac)}}{2a}เช่น ถ้าเราใช้ Excel กรอกสูตรนี้เข้าไปก็ชิลๆ เลย
x1 =(-B3-SQRT(B3^2-4*A3*C3))/(2*A3)
x2 =(-B3+SQRT(B3^2-4*A3*C3))/(2*A3)
โดยที่ A3=a, B3=b, C3=c ของสมการ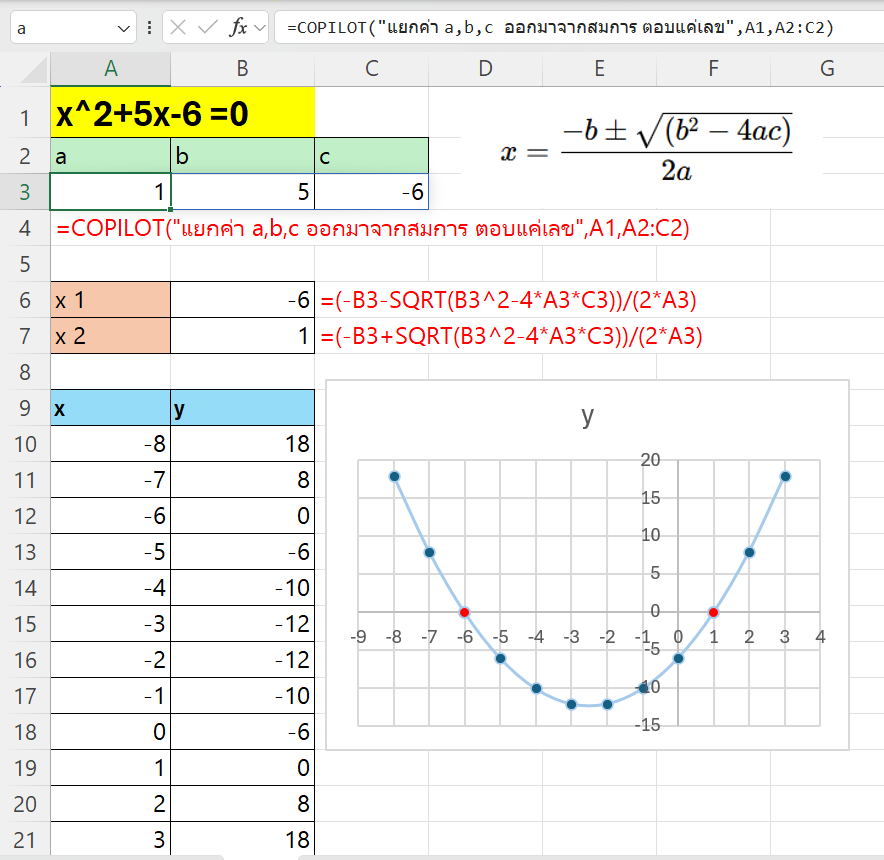
คำตอบก็จะออกมาเป็น x=-6 กับ x=1 เช่นกัน ลองทำเป็นกราฟก็ยิ่งชัด ว่ามันคือจุดที่กราฟตัดแกน x ซึ่งในที่นี้มีสองจุด
ถ้าเพื่อนๆ ขี้เกียจสร้างกราฟใน Excel ก็ลองใช้ Tools ของ web นี้ได้ครับ ดีเลย
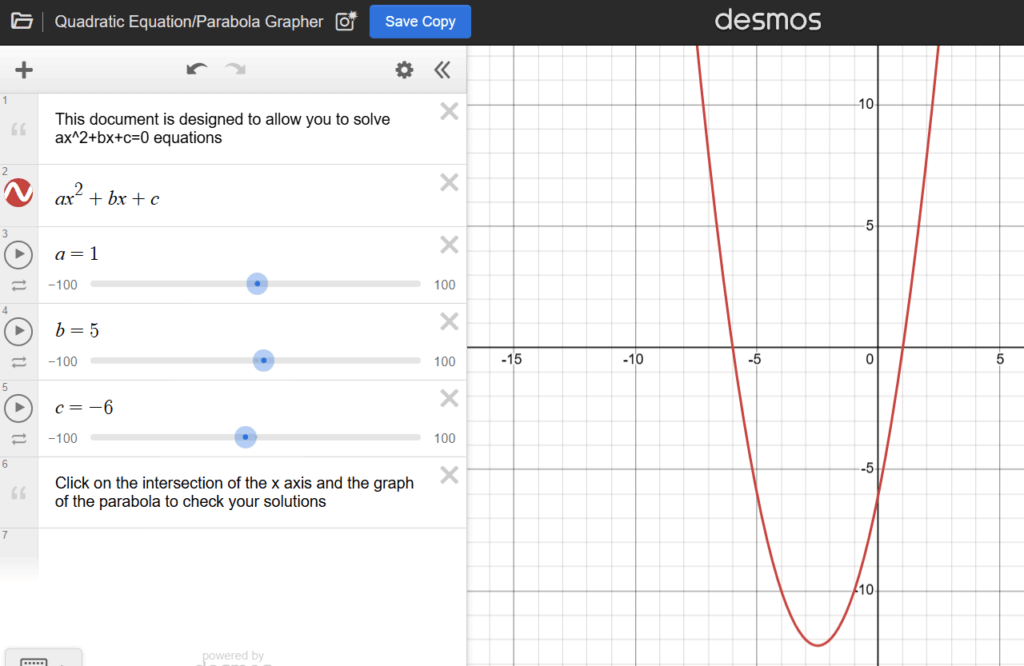
แต่ถ้าเรารู้ที่มาของมันซักหน่อยน่าจะดีกว่าครับ เผื่อเอาไว้อธิบายลูกหลานได้ด้วย
Standard Form
จริงๆ สมการมหัศจรรย์ มันก็เกิดจาก การจัดสมการพาราโบล่านี่แหละ ซึ่ง พาราโบลาในรูปมาตรฐาน (Standard Form) มีสมการดังนี้
y = ax^2 + bx + c
การจะแก้สมการหาค่า x ที่ทำให้ y เป็น 0 เราก็เลยเขียนได้ว่า
ax^2 + bx + c = 0
แล้วพยายามจัดรูป
x^2 + \frac{b}{a}x + \frac{c}{a} = 0พยายามให้อยู่ในรูปแบบกำลังสองสมบูรณ์
\left[ x^2 + 2x\left(\frac{b}{2a}\right) + \left(\frac{b}{2a}\right)^2 \right]
- \left(\frac{b}{2a}\right)^2 + \frac{c}{a} = 0\left( x + \frac{b}{2a} \right)^2 - \frac{b^2}{4a^2} + \frac{c}{a} = 0\left( x + \frac{b}{2a} \right)^2 - \frac{b^2 - 4ac}{4a^2} = 0ในที่สุดเราจะได้ค่า
x=\frac{-b±\sqrt{(b^2-4ac)}}{2a}แต่ไอ้วิธีพิสูจน์แบบนี้ มันดูทื่อๆ ไป ในความคิดของผม ผมคิดว่า ถ้าเราทำความเข้าใจในแง่ของกราฟมันจะเห็นภาพ และเข้าใจความหมายง่ายขึ้นเยอะ
Vertex Form
ซึ่งถ้าเราพยายามจัดกราฟ Parabola ให้อยู่ในรูปแบบ Vertex Form จะเห็นภาพชัดกว่า ซึ่งจะเกี่ยวข้องกับนิยามของ Parabola โดยแท้จริง นั่นก็คือ
พาราโบลา คือเซตของจุดทั้งหมดบนระนาบที่มีระยะจากจุด Focus เท่ากับระยะจากเส้นตรง Directrix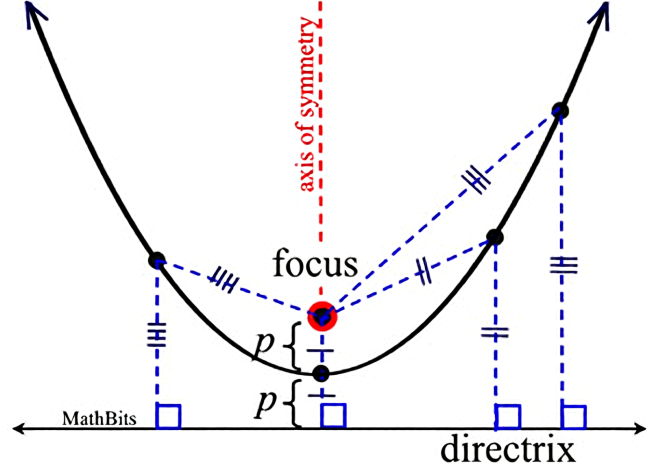
โดยที่ระยะห่างจาก Vertex (จุดยอดกราฟ) ไปถึงจุด Focus จะเรียกว่า p (ดังนั้นจาก Vertex ไปเส้น directrix ก็จะยาว p ด้วย)
เรามักจะเขียนกราฟ Parabola ให้อยู่ในรูปแบบนี้
ถ้าเราให้ h,k คือ พิกัดของจุดยอด Vertex ของกราฟพาราโบล่า จะทำให้เรารู้ตำแหน่ง Focus และสมการของ Directrix ไปด้วย
- vertex = (h,k)
- แกนสมมาตร คือ x=h
- focus ต้องเลื่อนขึ้นไปอีก p (จาก k) ทำให้ได้เป็น (h, k+p)
- directrix ต้องลงมาอีก p (จาก k) ทำให้ y=k-p

ทั้งหมดทำให้เขียนสมการอยู่ในรูปแบบนี้ได้
(x - h)^2 = 4p(y - k)
หรือถ้าย้ายข้างให้ y อยู่ข้างเดียวได้ว่า
(y−k)=\frac{1}{4p}(x−h)^2สามารถดูการพิสูจน์โดยใช้หลักการเรื่องระยะห่างเส้นตรงเท่ากันได้ที่นี่
แล้ว Vertex Form มันไปเกี่ยวกับ Standard Form ยังไง?
ตอนนี้เรารู้แล้วว่า กราฟพาราโบล่าสามารถเขียนได้ในรูปแบบ Vertex Form แล้วมันกลับไปผูกกับรูปแบบ Standard Form ยังไง? มาดูกันทีละขั้นตอน
สมการตอนแรกจะเป็น
(y−k)=\frac{1}{4p}(x−h)^2หรือ
y=\frac{1}{4p}(x−h)^2 + kซึ่งหน้าตาเหมือนกับ
y= ax^2+bx+c
ดังนั้น เราจะเทียบหาค่า a ได้เลย
a=\frac{1}{4p}หรือเราจะเขียน Vertex Form แบบที่มี a แทน p ก็ได้
y=a(x−h)^2 + k
ความหมายของ a,b,c
a = ตัวกำหนด “ความโค้ง” และ “ทิศทาง”
y= ax^2
- ถ้า a>0 → พาราโบลาหงายขึ้น
- ถ้า a=0 → กลายเป็นกราฟเส้นตรงแบนราบ (ไม่ใช่พาราโบล่า)
- ถ้า a<0 → พาราโบลาคว่ำลง
- ถ้า a ติดลบ p ก็จะติดลบ ทำให้ จุด focus มันมาอยู่ข้างล่างของ vertex นั่นเอง
- ยิ่ง |a| มาก → กราฟจะแคบลง
- ยิ่ง |a| เล็ก → กราฟจะกว้างออก
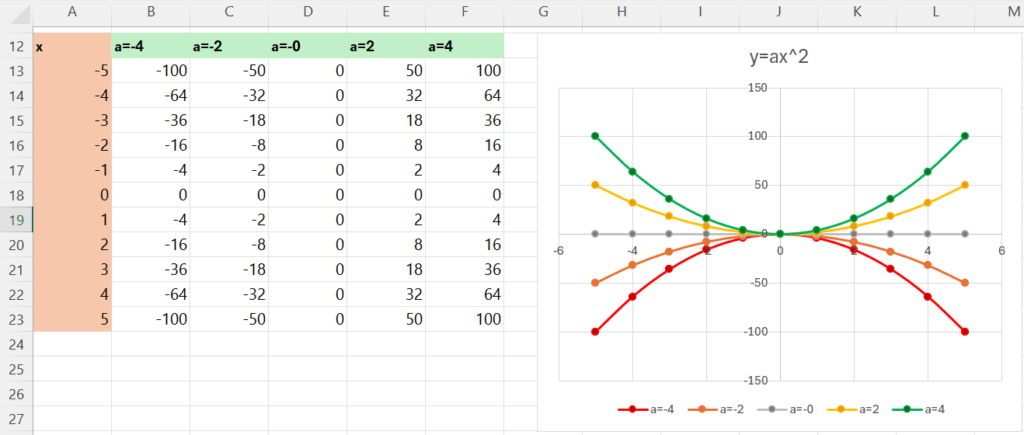
สรุปง่ายๆ: a คุม “รูปร่าง” ของพาราโบลา อันนี้น่าจะเข้าใจง่าย จำง่ายนะครับ
ต่อไป มาดูตัว b กับ c กันต่อ
จาก
y=a(x−h)^2+k
ถ้าเรากระจายออกมา จะได้ว่า
y = a(x^2-2hx+h^2) + k
จัดกลุ่มยกกำลัง
y=ax^2−2ahx+(ah^2+k)
แบบนี้แปลว่า
b=-2ah
c=ah^2+k
ทำให้มองในทางกลับกันได้ว่า
h=\frac{-b}{2a}k=c−\frac{b^2}{4a}ถ้าพิจารณาแบบนี้
b = ตัวที่มีผลในการเลื่อนแกนซ้ายขวา
โดยทิศทางของ b ตรงข้ามค่าของ a
- ถ้า a เป็น + : ยิ่ง b มาก = x เลื่อนซ้าย (h ติดลบเยอะ)
- ถ้า a เป็น – : ยิ่ง b มาก = x เลื่อนขวา (h + มาก)
- ถ้า b เป็น 0 จะทำให้ h = 0 (แกนสมมาตรอยู่เส้นดิ่งตรงกลาง)
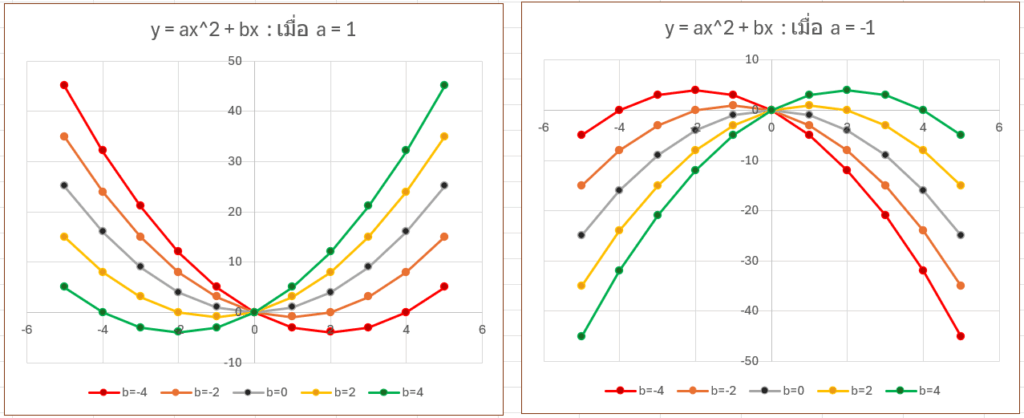
c = ตัวที่เลื่อนกราฟขึ้นลง และเป็นตัวกำหนด “จุดตัดแกน y” ด้วย
ส่วนตัว c นั้นพิจารณาง่าย เพราะ จาก
y = ax^2 + bx + c
ค่า c มันจะ adjust กราฟให้สูงขึ้น หรือ ต่ำลง (เพราะมัน + – ค่าเข้าไปให้ y ทื่อๆ เลย)
- ถ้า c เป็น + : กราฟเลื่อนขึ้น
- ถ้า c เป็น – : กราฟเลื่อนลง
และถ้าเรา set ให้ x เป็น 0 ค่า c จะ บอกได้เลยว่ากราฟ “ตัดแกน y” ที่ตรงไหน
ดังนั้น c = ตัวที่เลื่อนกราฟขึ้นลง และเป็นตัวกำหนด “จุดตัดแกน y” ด้วย
จะเห็นว่าค่า c จะกำหนดจุดตัดแกน y เสมอ
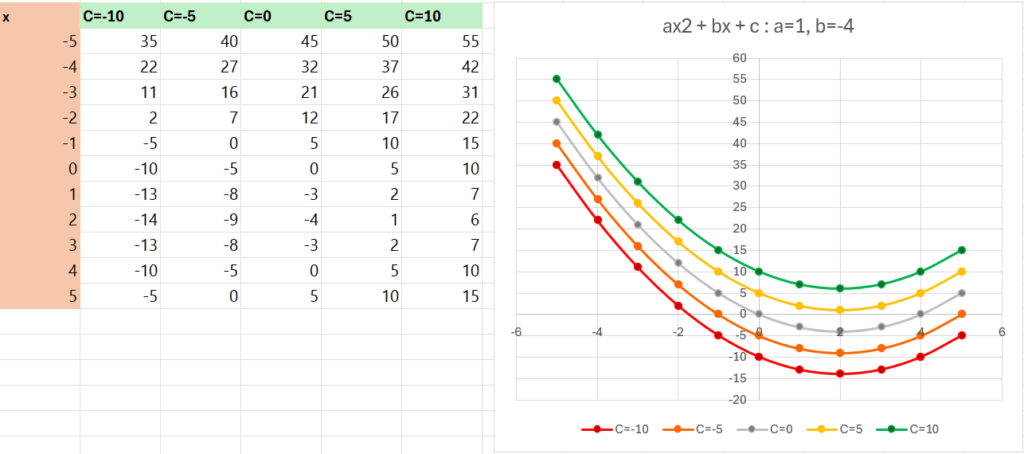
ถ้า a=1, b = 0 (เหลือแค่ y= x^2 + c)
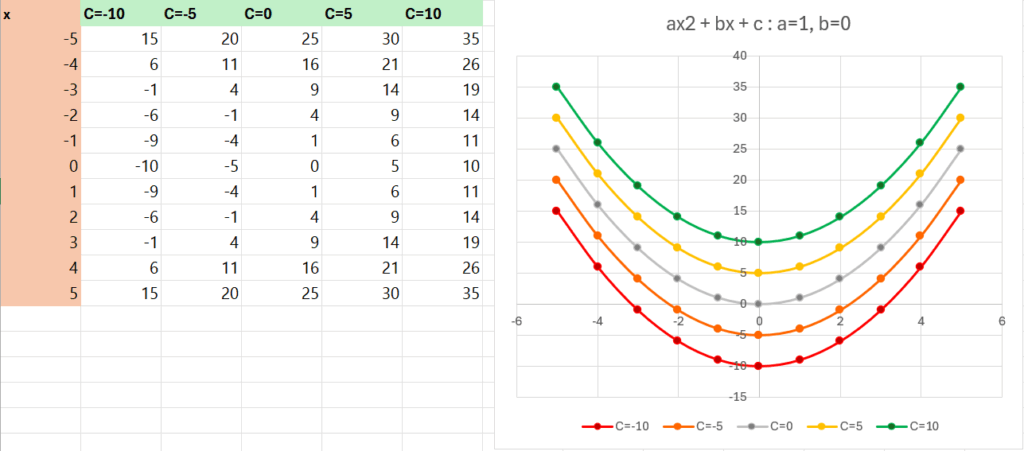
แม้ว่า ถ้า a=1, b = 4 (กราฟเลื่อนมาซ้าย เพราะ a เป็นบวก b เป็นบวก)
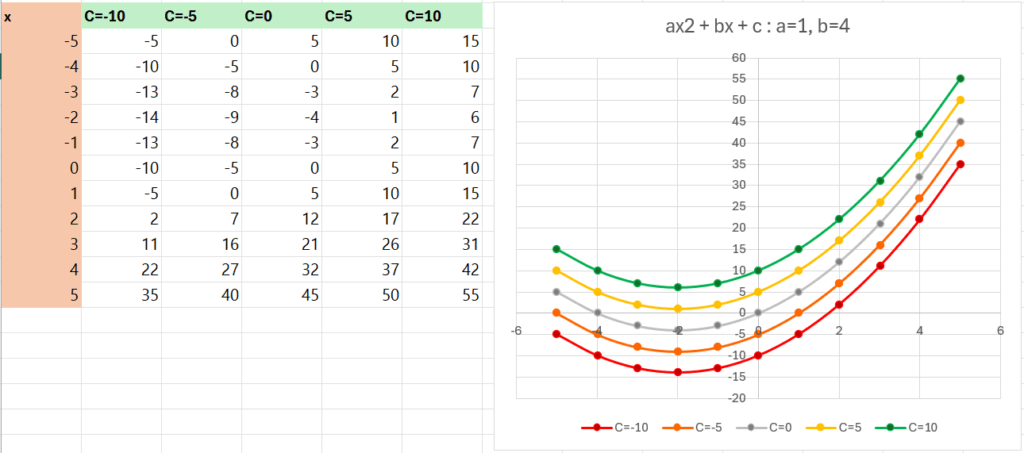
หรือ ถ้า a=1, b = -4 (กราฟเลื่อนมาขวา เพราะ a เป็นบวก b เป็นลบ)
ถ้ามองกลับกัน
จาก standard form
y=ax^2+bx+c
หากเราใช้ calculus (ถ้าใครยังไม่ได้เรียนไม่ต้องซีเรียส) หาจุดต่ำสุดสูงสุด โดยหา dy/dx ซึ่งคือความชัน โดยตั้งให้ =0 เพื่อหาจุดสูงสุด/ต่ำสุด
2ax+b=0
ดังนั้น
นี่แหละคือพิกัด x ของจุดยอด (vertex) หรือค่า h นั่นเอง
h = x = \frac{-b}{2a}แทนค่ากลับเข้าไปในสมการเดิม เพื่อหาค่า y ของ vertex
แทนค่ากลับเข้าไปในสมการเดิม เพื่อหาค่า y
y = a\left(-\frac{b}{2a}\right)^2 + b\left(-\frac{b}{2a}\right) + cy = \frac{4ac - b^2}{4a}หรือเขียนอีกแบบว่า
y = k = c - \frac{b^2}{4a}ลองพิจารณาความหมายของการแก้สมการ
จาก
(x - h)^2 = 4p(y - k)
ถ้าเราหาค่า x ที่ทำให้ y เป็น 0 ดังนั้นเราแทนค่า y= 0 ลงไป
(x - h)^2 = -4pk
ย้ายข้างให้เหลือ x ตัวเดียว
x=h±\sqrt{-4pk}ดังนั้นคำตอบของกราฟ Parabola มีแกนสมมาตรอยู่ที่ x=h แล้วแผ่ขยายออกไปข้างๆ ด้วยขนาด sqrt(-4pk)
ซึ่งเราถอดรากจริงได้เฉพาะเมื่อค่าข้างในรูท ≥ 0
ดังนั้น:
- ถ้า p>0 (พาราโบลาหงายขึ้น) → ต้องมี k≤0 (จุดยอดอยู่ต่ำ) ถึงจะตัดแกน x ได้
- ถ้า p<0 (พาราโบลาคว่ำลง) → ต้องมี k≥0 (จุดยอดอยู่สูง) ถึงจะตัดแกน x ได้
ซึ่งสอดคล้องกับภาพที่ vertex อยู่เหนือหรือใต้แกน x พอดี
ถ้าเขียนในรูปของ a,b,c คือ
h = \frac{-b}{2a},-4p = \frac{-1}{a},k=c-b^2/4aจัด k ดีๆ
-4p = \frac{-1}{a},k =\frac{4ac - b^2}{4a}คำนวณ -4pk
-4pk = \frac{b^2-4ac}{4a^2}\sqrt{-4pk} = ระยะจากจุดกึ่งกลาง = \frac{\sqrt{b^2-4ac}}{2a}จุดกลางแกนสมมาตร = \frac{-b}{2a}x = จุดกลาง ± ระยะจากแกนสมมาตร
x=\frac{-b}{2a}±\frac{\sqrt{(b^2-4ac)}}{2a}สุดท้ายมันก็มองเป็นสมการมหัศจรรย์ได้นั่นเอง
x=\frac{-b±\sqrt{(b^2-4ac)}}{2a}สรุป
สรุปสมการ parabora
standard form
y=ax^2+bx+c
vertex form
(x - h)^2 = 4p(y - k)
y = a(x - h)^2 + k
สรุปแต่ละสัญลักษณ์:
| ตัวแปร | บอกอะไร | สูตรเทียบกับอีกตัว |
|---|---|---|
| a | ทิศทางและความโค้ง (หงาย/คว่ำ, แคบ/กว้าง) | a = 1/(4p) เฉพาะกรณีกราฟแนวตั้ง |
| b | การเลื่อนซ้าย–ขวา | b = -2ah |
| c | การเลื่อนขึ้น–ลง จุดตัดแกน y | c = ah^2+k |
| h | ค่า x ของจุดยอด (vertex) | h = -b/2a |
| k | ค่า y ของจุดยอด (vertex) | k = c-b^2/4a |
| p | ระยะจาก vertex ไป focus | p = 1/(4a) เฉพาะกรณีกราฟแนวตั้ง |
สรุปแก้สมการ
หาค่า x ที่ทำให้ y =0
x=h±\sqrt{-4pk}x=\frac{-b±\sqrt{(b^2-4ac)}}{2a}จำนวนคำตอบของสมการ
เราสามารถมองได้ว่า ค่าภายในรูท (เรียกว่า Discriminant) คือ ค่าที่ช่วยบอกจำนวนคำตอบของสมการได้
- ถ้า > 0 จะทำให้ x มี 2 คำตอบ
- กราฟตัดแกน x สองจุด
- ถ้า = 0 จะทำให้ x มีคำตอบเดียว
- กราฟสัมผัสแกน x พอดีที่ vertex นั่นคือ x=h หรือ -b/2a
- ถ้า < 0 ระยะเป็นจำนวนจินตภาพ (ไม่จริง) ไม่มีคำตอบที่เป็นเลขจำนวนจริง
- กราฟไม่ตัดแกน x นั่นเอง