TL;DR: เทียบบัญญัติไตรยางค์ใช้ได้เมื่อ “อัตราคงที่” เท่านั้น เช่น ราคาต่อหน่วยคงที่ ถ้าคน 3 คนทำงาน 45 นาที แล้ว 5 คนจะใช้เวลาเท่าไหร่? คำตอบไม่ใช่ 75 นาที แต่เป็น 27 นาที เพราะคนมากขึ้น = เร็วขึ้น ไม่ใช่ช้าลง! บทความนี้จะสอนให้เข้าใจ “ความจริง” ก่อนสูตร
ที่ผมเขียนบทความนี้ขึ้นมา เพราะผมดันไปเจอโพสต์สอนสูตร Excel แค่บวกลบคูณหารธรรมดา แต่มีคนแชร์เป็นพัน! เลยรู้สึกว่าคนไทยอาจมีปัญหากับคณิตศาสตร์พื้นฐานหนักกว่าที่คิด 😅
ผมเลยอยากชวนมาทบทวนหลักการคณิตศาสตร์ง่ายๆ อย่าง “เทียบบัญญัติไตรยางค์” ให้เข้าใจให้ถึงแก่น ว่ามันคืออะไร ทำงานยังไง ทำไมต้องคูณไขว้ แล้วแบบไหนใช้ได้หรือไม่ได้กันแน่
เพราะจากที่ผมสอนมา เด็กๆ (หรือแม้แต่ผู้ใหญ่หลายคน) มักใช้วิธีตั้งเลขแล้วคูณไขว้ตามแพตเทิร์นโดยไม่รู้ว่ามันหมายถึงอะไร ใช้ถูกบ้างผิดบ้าง ทั้งที่จริงๆ แล้วทุกโจทย์มี “ความจริงเดียว” ซ่อนอยู่ (แค่เรายังอาจมองเห็นมันไม่ชัดเจนพอ)
ดังนั้น ถ้ามีลูกหลาน (หรือแม้แต่ตัวเอง) ที่ยังงงๆ กับเรื่องนี้ ลองอ่านดูครับ อ่านจบรับรองเข้าใจแน่นอน!
เทียบบัญญัติไตรยางค์ คืออะไร?
มันคือวิธีคิดทางคณิตศาสตร์เวลาเรา รู้ของอยู่ 3 อย่าง (ไตรยางค์) แล้วอยากหาของอย่างที่ 4 ที่เกี่ยวข้องกัน โดยมีเงื่อนไขคือ สิ่งเหล่านั้นมีความสัมพันธ์แบบคงที่ (เพิ่มหรือลดในอัตราเดียวกัน) ซึ่งภาษาอังกฤษจะตรงกับคำว่า Rule of Three นะครับ
วิธีทำเทียบบัญญัติไตรยางค์ (แบบสั้นๆ)
- หาสิ่งที่คงที่ – ถามตัวเองว่า “อะไรคือความจริงที่ไม่เปลี่ยน?”
- คำนวณค่าต่อหน่วย – หารเพื่อหาค่าต่อ 1 หน่วย
- คูณกลับ – เอาค่าต่อหน่วยคูณจำนวนที่ต้องการ
ตารางสรุป: ใช้ไตรยางค์ได้ vs ไม่ได้
| สถานการณ์ | ใช้ไตรยางค์ได้? | เหตุผล |
|---|---|---|
| ซื้อของราคาต่อชิ้นคงที่ | ✅ ได้ | ราคาต่อหน่วยคงที่ |
| คนทำงานช่วยกัน | ❌ ไม่ได้ตรงๆ | คนมากขึ้น = เวลาน้อยลง (แปรผกผัน) |
| ขับรถความเร็วคงที่ | ✅ ได้ | ระยะทาง ∝ เวลา |
| ค่าส่งแบบขั้นบันได | ❌ ไม่ได้ | อัตราไม่คงที่ |
| แลกเงินอัตราคงที่ | ✅ ได้ | อัตราแลกเปลี่ยนคงที่ |
| ดอกเบี้ยทบต้น | ❌ ไม่ได้ | อัตราเพิ่มขึ้นแบบ exponential |
ความจริงก่อนสูตร
ทุกสมการในโลกนี้ ล้วนเป็นเพียง “ภาษาที่เขียนความจริงออกมาให้สั้นลง” เท่านั้นเอง
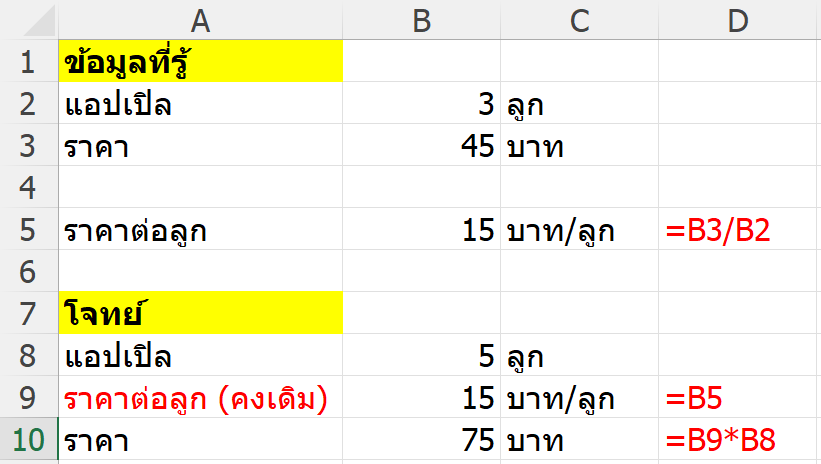
โจทย์แอปเปิล (แปรผันตรง)
ถ้าเราซื้อแอปเปิล 3 ลูก ราคา 45 บาท
ถ้าซื้อ 5 ลูก จะต้องจ่ายเท่าไร?
หลายคนที่จำสูตรได้ จะรีบคูณไขว้ทันทีแบบนี้
จ่าย = 45/3 x 5 = 75 บาท
ซึ่งก็ได้ค่าที่ถูกต้อง แต่มันจะแย่ถ้าเราไม่เข้าใจว่าทำไมถึงทำแบบนั้นได้?
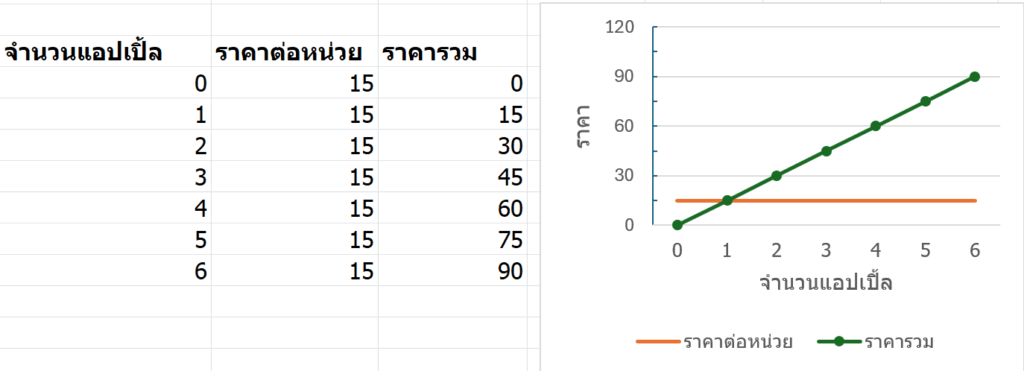
ความจริงที่ควรยึด: ราคาแอปเปิ้ล (ต่อชิ้น) นั้นคงที่
- แอปเปิล 3 ลูก = 45 บาท
- ดังนั้น 1 ลูก = 45/3 = 15 บาท (นี่คือสิ่งที่คงที่!)
- ถ้าซื้อ 5 ลูก = 15 × 5 = 75 บาท
สูตรใน Excel:
=ราคาที่รู้ / จำนวนที่รู้ * จำนวนที่ต้องการ
=45/3*5
โจทย์คนทำงาน (แปรผกผัน) ⚠️
คน 3 คน ใช้เวลาทำงานให้เสร็จ 45 นาที
ถ้า 5 คนช่วยกัน จะใช้เวลาเท่าไหร่?
ถ้าใครเผลอไปทำแบบเดิม คือ คิดว่า
ใช้เวลา 45/3 x 5 = 75 นาที แบบนี้คือผิดไปเลย! ❌
เพราะโจทย์ข้อนี้เป็น ความสัมพันธ์แบบแปรผกผัน จะมาใช้บัญญัติไตรยางค์แบบปกติไม่ได้
ซึ่งจริงๆ แค่ใช้ common sense คิดก็ควรจะเอะใจแล้วว่า ถ้ามีคนมาช่วยทำงานเยอะขึ้น มันต้องทำงานเสร็จเร็วขึ้น (ใช้เวลาน้อยลง) สิ ไม่ใช่ทำงานช้าลง (ใช้เวลามากขึ้น) ยกเว้นว่าคนจะมาขัดแข้งขัดขากันเองนั่นอีกเรื่องนึง 😂
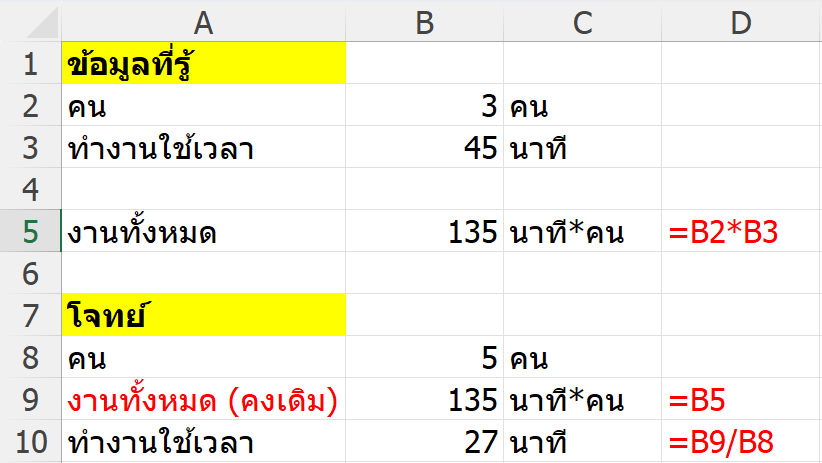
ความจริงที่ควรยึด: ปริมาณงาน (ทั้งหมด) ที่ต้องทำ นั้นคงที่
- คน 3 คน ใช้เวลา 45 นาที = งานเท่ากับคน 1 คนทำ 3 × 45 = 135 คน-นาที
- ถ้ามี 5 คน = 135 / 5 = 27 นาที ✅
สูตรใน Excel:
=จำนวนคนเดิม * เวลาเดิม / จำนวนคนใหม่
=3*45/5

สิ่งที่ทุกคนต้องคิดและต้องยึดถือ คือ “อะไรคือความจริง?” ต่างหาก ไม่ใช่การจำสูตรหรือจำสมการอะไรทั้งนั้น
โจทย์ค่าส่งพัสดุ (อัตราแบบขั้นบันได) ⚠️
ส่งของราคาไม่เกิน 2 ชิ้น ชิ้นละ 30 บาท
ส่งเพิ่มจากนั้น ชิ้นละ 10 บาท
ถ้าส่ง 5 ชิ้น ค่าส่งทั้งหมดเท่าไร?
จะเห็นว่า ถ้าเรารีบเทียบบัญญัติไตรยางค์เลยว่า
ส่งของ 2 ชิ้น = 60 บาท
ดังนั้น 5 ชิ้น = 60/2 × 5 = 150 บาท
แบบนี้คือ “ผิดทันที” ❌
เพราะค่าส่งไม่ได้เพิ่มในอัตราคงที่ แต่มี “ขั้นบันได” (step rate)
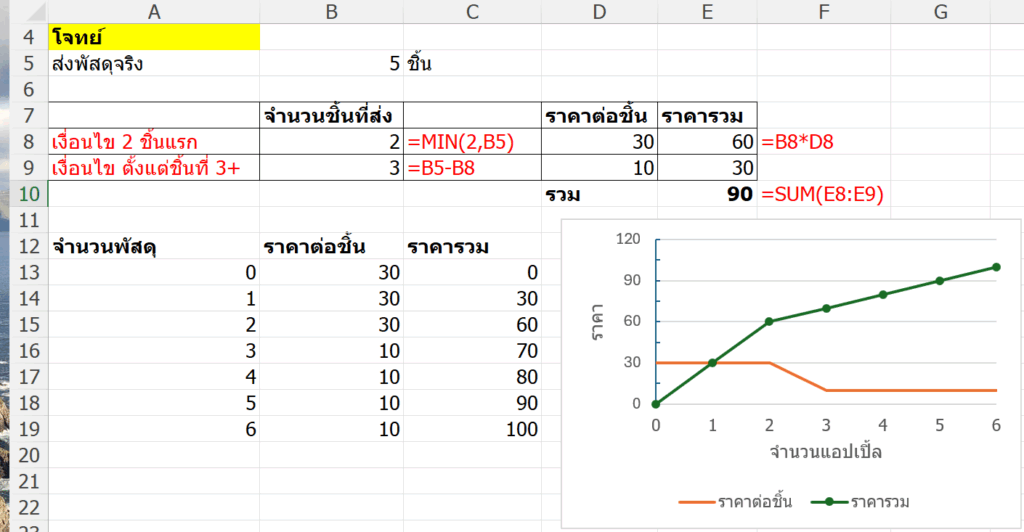
ความจริงที่ต้องยึด: ราคาต่อหน่วยเป็นแบบขั้นบันได
- 2 ชิ้นแรก : 2 × 30 = 60 บาท
- 3 ชิ้นที่เหลือ : 3 × 10 = 30 บาท
- รวมทั้งหมด = 60 + 30 = 90 บาท ✅
สูตรใน Excel:
=MIN(จำนวน,2)*30 + MAX(จำนวน-2,0)*10
=MIN(5,2)*30 + MAX(5-2,0)*10
ข้อผิดพลาดที่พบบ่อย
| ข้อผิดพลาด | ปัญหา | วิธีแก้ |
|---|---|---|
| คูณไขว้โดยไม่คิด | ใช้สูตรโดยไม่เข้าใจความสัมพันธ์ | ถามตัวเองก่อนว่า “อะไรคงที่?” |
| สับสนแปรผันตรง/ผกผัน | คนมากขึ้น ≠ เวลามากขึ้น | ใช้ common sense ตรวจสอบ |
| ลืมเช็คอัตราคงที่ | ใช้ไตรยางค์กับขั้นบันได | ตรวจสอบก่อนว่าอัตราเปลี่ยนไหม |
| จำแค่สูตร ไม่เข้าใจที่มา | ใช้ถูกบ้างผิดบ้าง | เข้าใจ “ความจริง” ของโจทย์ |
ตัวอย่างเพิ่มเติมพร้อมเฉลย
ตัวอย่าง 1: แลกเงิน
ถ้า 100 บาท แลกได้ 2.8 ดอลลาร์
500 บาท จะแลกได้กี่ดอลลาร์?
ความจริง: อัตราแลกเปลี่ยนคงที่
วิธีทำ:
– 1 บาท = 2.8/100 = 0.028 ดอลลาร์
– 500 บาท = 0.028 × 500 = 14 ดอลลาร์ ✅
ตัวอย่าง 2: ขับรถ
ขับรถ 2 ชั่วโมง ได้ระยะทาง 160 กม.
ถ้าขับ 5 ชั่วโมง (ความเร็วเท่าเดิม) จะได้กี่ กม.?
ความจริง: ความเร็วคงที่
วิธีทำ:
– ความเร็ว = 160/2 = 80 กม./ชม.
– 5 ชั่วโมง = 80 × 5 = 400 กม. ✅
ตัวอย่าง 3: ก๊อกน้ำ (แปรผกผัน)
ก๊อกน้ำ 2 ก๊อก เปิดเติมน้ำเต็มถัง 30 นาที
ถ้าเปิด 3 ก๊อก จะใช้เวลาเท่าไหร่?
ความจริง: ปริมาณน้ำที่ต้องเติมคงที่
วิธีทำ:
– ปริมาณงาน = 2 × 30 = 60 ก๊อก-นาที
– 3 ก๊อก = 60 / 3 = 20 นาที ✅
โจทย์ฝึกทำด้วยตัวเอง
ลองทำดูครับ! เฉลยอยู่ด้านล่าง
ข้อ 1: ซื้อไข่ 12 ฟอง ราคา 60 บาท ถ้าซื้อ 20 ฟอง จ่ายเท่าไหร่?
ข้อ 2: ช่าง 4 คน ซ่อมบ้านเสร็จใน 6 วัน ถ้ามี 3 คน จะใช้เวลากี่วัน?
ข้อ 3: ค่าแท็กซี่: 2 กม.แรก 35 บาท กม.ละ 5 บาทหลังจากนั้น ถ้านั่ง 10 กม. จ่ายเท่าไหร่?
ข้อ 4: ถ้า 3 ลิตร ราคา 150 บาท 7 ลิตรราคาเท่าไหร่?
ข้อ 5: เครื่องจักร 5 เครื่อง ผลิตของ 100 ชิ้น/ชม. ถ้ามี 8 เครื่อง จะผลิตได้กี่ชิ้น/ชม.?
คลิกดูเฉลย
**ข้อ 1:** 60/12 × 20 = **100 บาท** (ราคาต่อฟองคงที่)
**ข้อ 2:** 4 × 6 / 3 = **8 วัน** (ปริมาณงานคงที่ – แปรผกผัน)
**ข้อ 3:** 35 + (10-2) × 5 = 35 + 40 = **75 บาท** (ขั้นบันได – ใช้ไตรยางค์ไม่ได้!)
**ข้อ 4:** 150/3 × 7 = **350 บาท** (ราคาต่อลิตรคงที่)
**ข้อ 5:** 100/5 × 8 = **160 ชิ้น/ชม.** (กำลังผลิตต่อเครื่องคงที่)
สูตร Excel สำหรับไตรยางค์
แปรผันตรง (Direct Proportion)
=ค่าที่รู้ / จำนวนที่รู้ * จำนวนที่ต้องการ
แปรผกผัน (Inverse Proportion)
=จำนวนเดิม * ค่าเดิม / จำนวนใหม่
ขั้นบันได (Step Rate)
=MIN(จำนวน, เกณฑ์) * ราคาช่วงแรก + MAX(จำนวน-เกณฑ์, 0) * ราคาช่วงหลัง
คำถามที่พบบ่อย (FAQ)
Q: เทียบบัญญัติไตรยางค์ ภาษาอังกฤษเรียกว่าอะไร?
A: Rule of Three หรือ Cross-multiplication method
Q: ไตรยางค์ใช้ได้เมื่อไหร่?
A: ใช้ได้เมื่ออัตราคงที่ เช่น ราคาต่อหน่วยคงที่ ความเร็วคงที่ อัตราแลกเปลี่ยนคงที่
Q: ไตรยางค์ใช้ไม่ได้เมื่อไหร่?
A: ใช้ไม่ได้เมื่ออัตราไม่คงที่ เช่น ค่าส่งแบบขั้นบันได ดอกเบี้ยทบต้น หรือความสัมพันธ์แบบแปรผกผัน
Q: จะรู้ได้ยังไงว่าแปรผันตรงหรือแปรผกผัน?
A: ใช้ common sense! ถ้าอย่างหนึ่งมากขึ้น อีกอย่างก็มากขึ้น = แปรผันตรง ถ้าอย่างหนึ่งมากขึ้น อีกอย่างน้อยลง = แปรผกผัน
สรุป
สรุปแล้ว ผมว่าอย่าไปสนใจสูตรหรือคำว่า “เทียบบัญญัติไตรยางค์” มากนักเลยครับ
สิ่งที่สำคัญกว่าคือ เราเข้าใจหรือยังว่า…
- อะไรมันสัมพันธ์กับอะไร
- ธรรมชาติของสิ่งนั้นคืออะไร
- แล้ว “อะไรคือความจริง” ของโจทย์นั้นกันแน่
ความจริงเหล่านี้มักซ่อนอยู่ในรูปแบบของ “สิ่งที่คงที่” หรือ “หลักการที่แน่นอน”
เราแค่ต้องจับให้ได้ว่ามันคืออะไร
เมื่อเข้าใจสามข้อนี้แล้ว เราก็สามารถเขียนความสัมพันธ์ออกมาเป็นสมการของเราเองได้ โดยไม่ต้องท่องจำสูตรใดๆ เลย
แต่ถ้าจะใช้ “เทียบบัญญัติไตรยางค์” จริงๆ มันใช้ได้เฉพาะใน กรณีที่ความสัมพันธ์เป็นเส้นตรง (อัตราคงที่) เท่านั้น เช่น ราคาต่อหน่วยคงที่, ความเร็วคงที่, หรืออัตราการผลิตคงที่
แต่ถ้าเมื่อไหร่ “อัตราเปลี่ยนกลางทาง” หรือมี “ขั้นบันได / เงื่อนไขพิเศษ” นั่นแปลว่า “ความจริงไม่คงที่” แล้ว
อย่าเพิ่งรีบคูณไขว้ครับ… ให้หยุดก่อน แล้วถามตัวเองว่า
“โจทย์นี้ ความจริงคืออะไรกันแน่? เรารู้ธรรมชาติอะไรของมันบ้าง?”
เพียงแค่เปลี่ยนจาก “จำสูตร” เป็น “มองความจริง” คณิตศาสตร์ก็จะไม่ใช่ของยากอีกต่อไปครับ เพราะสุดท้ายแล้ว… คณิตศาสตร์ก็คือภาษาที่ใช้อธิบายความจริงของจักรวาล เราแค่หาความจริงให้ได้เท่านั้นเองครับ 🙂
Last updated: ธันวาคม 2025



