Statistics with Excel ตอนที่ 1 : ค่าสถิติที่สำคัญ

Statistics (สถิติ) นั้นเป็นศาสตร์ที่สามารถช่วยให้เราเปลี่ยนข้อมูลดิบ (Data) ให้เป็นข้อมูลที่มีประโยชน์ (Information) ได้ ซึ่งมีความจำเป็นและมีประโยชน์มากต่อการช่วยให้เราสามารถตัดสินใจด้วยข้อมูลได้ดีขึ้น เหมาะกับองค์กรในยุคปัจจุบันที่ต้องใช้ Data ในการตัดสินใจ หรือที่เรียกว่า Data-Driven Organization

ซึ่งในซีรีส์นี้เราจะมาเรียนรู้เรื่องสถิติกันตั้งแต่พื้นฐานกันเลยครับ

Version VDO บน YouTube (ฝาก subscribe ด้วยน้าาาา)

ภาพรวมของสถิติ

• Descriptive Statistics (สถิติเชิงพรรณนา) = การสร้างตัวเลขมาบรรยายลักษณะข้อมูลที่มีอยู่ในรูปแบบของผลสรุปต่างๆ ไม่ว่าจะมาจากข้อมูลทั้งหมดหรือมาจากกลุ่มตัวอย่างก็ตาม ซึ่งสามารถแบ่งการสรุปออกเป็น 2 กลุ่มใหญ่ๆ คือ
  • Central Tendency (แนวโน้มค่ากลาง) เช่น Mean (ค่าเฉลี่ยเลขคณิต), Median (มัธยฐาน)
  • Dispersion (การกระจาย) เช่น Standard Deviation (ส่วนเบี่ยงเบนมาตรฐาน)
• Inferential Statistics (สถิติเชิงอนุมาน) = การนำข้อมูลจากตัวอย่างที่เก็บมาจำนวนน้อย ไปใช้อนุมาน (infer) เพื่อตอบคำถามเกี่ยวกับข้อมูลที่แท้จริงที่มีจำนวนมากกว่า ซึ่งเราไม่สามารถเก็บข้อมูลมาทั้งหมดได้จริงๆ โดยแบ่งเป็น
  • Estimation (การประมาณค่า) = การเอาข้อมูลจาก Sample ไปสรุปหรือประมาณค่าของข้อมูล Population
  • Hypothesis Testing (การทดสอบสมมติฐาน) = การใช้หลักการสถิติไปตอบคำถามที่เราสนใจ เช่น ยาตัวใหม่ได้ผลจริงๆ หรือแค่มโนไปเอง

นิยามของข้อมูลทางสถิติ

• ข้อมูลทั้งหมดที่เราสนใจเรียกว่า Population (ประชากร) ถ้าเราเลือกที่จะเก็บข้อมูล Population ทั้งหมดเลยเราจะเรียกข้อมูลนั้นว่า Census และสิ่งที่เป็นตัวแปรวัดค่าของมันจะเรียกว่า Parameter (ใช้ตัวอักษรกรีก)
• แต่ถ้าเราเก็บตัวอย่างมาบางส่วน (เนื่องจากเก็บหมดไม่ไหว) เราจะสิ่งที่เราเก็บมาว่า Sample (กลุ่มตัวอย่าง) และมีตัวแปรวัดค่าที่เรียกว่า Statistic (ใช้ตัวอักษรโรมัน)

ข้อมูลทางสถิตินั้นแบ่งได้เป็น 2 ประเภทใหญ่ๆ คือ

• Qualitative Data เมื่อข้อมูลนั้นถูกจัดอยู่ในประเภท หรือหัวข้อ เช่น สีต่างๆ, ผ่าน หรือ ตก, ต่ำ กลาง สูง และสามารถแบ่งย่อยออกเป็น 2 ประเภทคือ
  • Nominal = เมื่อการเรียงของข้อมูลไม่มีความหมาย เช่น สีแดง เหลือง เขียว (การเรียงของสีไม่มีความหมาย)
  • Ordinal = เมื่อการเรียงข้อมูลมีความหมาย เช่น ต่ำ กลาง สูง, หรือ เกรด A-F เป็นต้น
• Quantitative Data เมื่อข้อมูลนั้นสามารถนับหรือวัดได้ ซึ่งสามารถแบ่งย่อยออกเป็น 2 อย่างคือ
  • Discrete เมื่อข้อมูลนั้นวัดเป็นจำนวนเต็มได้เท่านั้น (สามารถนับเป็นชิ้นๆ ได้ เช่น จำนวนคนที่อยู่ในห้องเรียน)
  • Continuous เมื่อข้อมูลนั้นจะเป็นตัวเลขค่าอะไรก็ได้ (เช่น ส่วนสูง น้ำหนัก)

เอาล่ะเมื่อเห็นภาพรวมแล้ว ในตอนที่ 1 นี้เราจะมาเจาะลึกตัว Descriptive Statistics กัน และจะลองทำใน Excel กันด้วยครับ

ข้อมูลที่จะนำมาวิเคราะห์

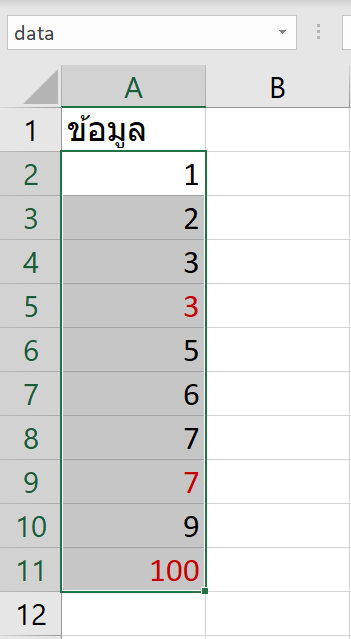
ซึ่งข้อมูลก็ไม่มีอะไรมากครับ ให้ทุกคนสร้างเลข running 1-10 ใน Excel (โดยใส่ 1 แล้วคลิ๊กขวาที่ Fill Handle แล้วลากลงมา) จากนั้นให้เปลี่ยนเลขบางส่วนดังต่อไปนี้

• เปลี่ยน 4 เป็นเลข 3
• เปลี่ยน 8 เป็นเลข 7
• เปลี่ยน 10 เป็น 100

สรุปจะได้ Data หน้าตาแบบนี้นะ ซึ่งผมตั้งชื่อ (Define Name) เจ้า Range A2:A11 นี้ ว่า data เพื่อให้ดูสูตรแล้วเข้าใจง่ายขึ้น และ copy paste ง่ายขึ้นด้วย

การคำนวณสุดฮิตที่ใช้ใน Descriptive Statistics

ปกติการทำผลสรุปทั้งสถิติต่างๆ เพื่ออธิบายลักษณะของข้อมูลนั้น มักจะแบ่งเป็น 2 กลุ่ม คือ

Central Tendency (แนวโน้มค่ากลาง)

ค่ากลางก็คือสิ่งที่จะทำหน้าที่เป็นตัวแทนข้อมูลของเราได้ ซึ่งจะเป็นตัวแทนที่ดีหรือไม่ก็ขึ้นกับการกระจายของข้อมูลด้วย

Mean (ค่าเฉลี่ยเลขคณิต)

คือ ค่าเฉลี่ยที่เกิดจากผลรวมข้อมูลทั้งหมดหารด้วยจำนวนข้อมูล นี่น่าจะเป็นค่าสถิติที่คนส่วนใหญ่รู้จักดีกันมากที่สุดเลยล่ะ
แต่มันมีข้อเสียที่สำคัญ คือ มันจะได้รับอิทธิพลจากค่าที่น้อยหรือเยอะมากๆ มาดึงค่าเฉลี่ยไป ทำให้อาจเข้าใจผิดได้ (เดี๋ยวจะได้เห็นว่าค่า 100 จะดึง Mean ขึ้นไปขนาดไหน หึหึ)

=AVERAGE(data)              // Excel จะคำนวณเฉพาะค่าที่เป็น Number เท่านั้น
=SUM(data)/COUNT(data)      // Excel จะคำนวณเฉพาะค่าที่เป็น Number เท่านั้น

Median (มัธยฐาน)

คือ ค่าที่อยู่ตำแหน่งกึ่งกลาง เมื่อนำข้อมูลมาเรียงกันจากน้อยไปมาก
ดีตรงที่แทบไม่ได้รับอิทธิผลจากค่ามากหรือน้อยจัดๆ

= MEDIAN(data)

Mode (ฐานนิยม)

คือ ค่าที่เกิดขึ้นบ่อยที่สุดในชุดข้อมูล อาจมีค่าเดียวหรือหลายค่าก็ได้
ข้อดีคือมั่นใจได้ว่าเป็นค่าที่มีอยู่จริงในข้อมูล ไม่เหมือน Mean ซึ่งอาจได้เลขที่ไม่มีอยู่จริงๆ

= MODE.SNGL(data)         // ใช้กรณีที่อยากได้ผลลัพธ์ค่าเดียว (MODE ใน version เก่าก็คือตัวนี้)
= MODE.MULT(data)         // สามารถแสดงผลลัพธ์หลายค่าได้ (ออกมาเป็น array)

เมื่อทดลองกับข้อมูลของเราแล้วจะได้ผลลัพธ์แบบนี้ครับ

Dispersion (การกระจาย)

เป็นการวัดว่าข้อมูลเรามีการกระจายตัวมากน้อยแค่ไหน ยิ่งถ้ามีการกระจายมาก ค่ากลางที่ได้ก็อาจจะไม่ใช่ตัวแทนของข้อมูลได้ดีนัก

Range (พิสัย)

วัดการกระจายโดยเอาค่ามากสุด – ค่าน้อยสุด

=MAX(data) - MIN(data)

Variance (ความแปรปรวน)

วัดการกระจายโดยเอาความต่างของแต่ละจุดข้อมูลกับค่าเฉลี่ยมากยกกำลังสอง แล้วหาค่าเฉลี่ย
(ที่ใช้วิธียกกำลังสองเพื่อแก้ปัญหาเรื่องเครื่องหมายบวกลบ และลงโทษค่าที่ไกลจากค่า Mean มากๆ ได้ดีกว่าการหาค่า Absolute)

=VAR.P(range)      //ใช้กับข้อมูลที่มาจาก Population ทั้งหมด
=VAR.S(range)      //ใช้กับข้อมูลที่มาจาก Sample (มีการแยกสูตรเพราะถ้าคำนวณตามปกติค่าที่ได้จะน้อยเกินจริง เลยพยายาม adjust สูตรให้ตัวหารน้อยลง ค่าที่จะได้จะเยอะขึ้นจนใกล้เคียงค่าจริงของ Population มากขึ้น)

ถ้าดูสูตรทางคณิตศาสตร์จริงๆ แล้วก็จะงงๆ หน่อย แต่มันหมายถึงสิ่งที่ผมเขียนไปข้างบนนี่แหละ จะเข้าใจได้มากขึ้นผมอยากให้ดูรูปนี้ครับ สมมติว่าเส้นสีดำตรงกลางคือค่าเฉลี่ยของข้อมูล

เมื่อเราเอาระยะห่างของแต่ละจุดกับค่าเฉลี่ย มายกกำลังสอง ก็จะได้พื้นที่สี่เหลี่ยม จากนั้นเอาขนาดสี่เหลี่ยมทุกอันมาเฉลี่ยกันจะได้ Variance นั่นเอง

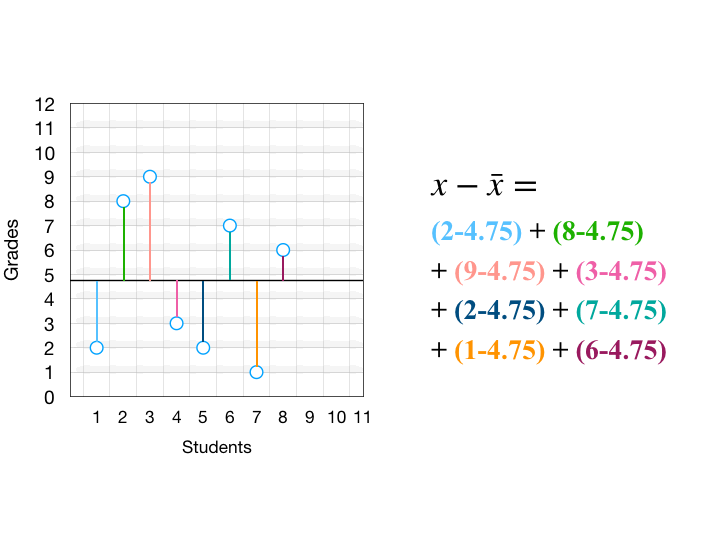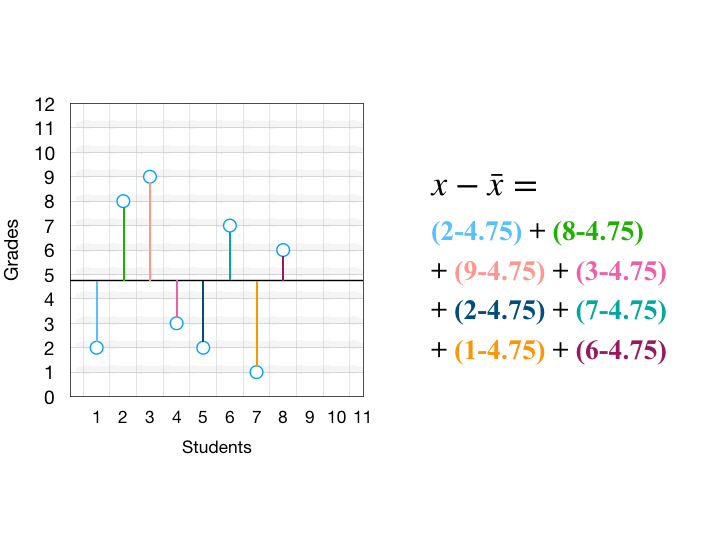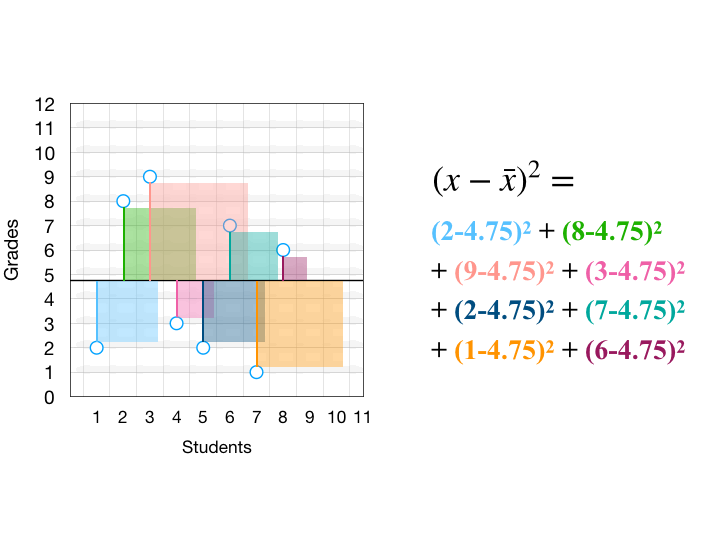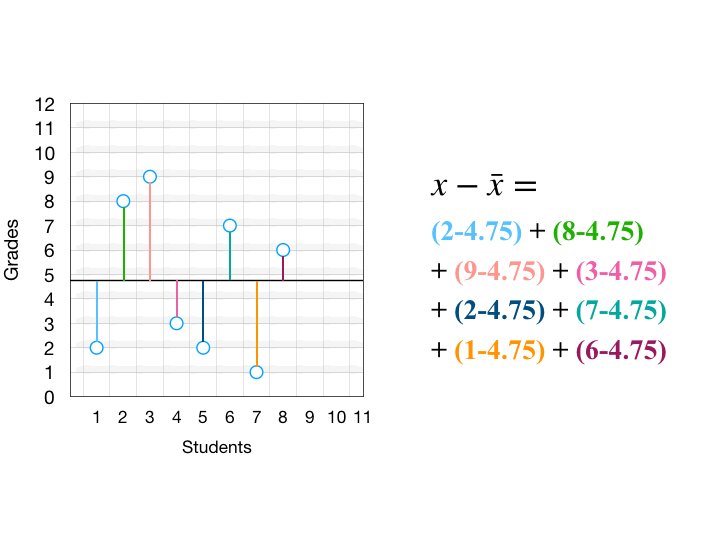
ข้อเสียของ Variance คือ มีปัญหาเรื่องหน่วยที่ไม่เหมือนกับ Data ต้นฉบับ (เพราะดันมีการยกกำลังสอง)

Standard Deviation (ส่วนเบี่ยงเบนมาตรฐาน)

คือการเอาค่า Variance มาหารากที่สอง เพื่อแก้ปัญหาเรื่องหน่วยให้ได้หน่วยเดียวกับ Data จริงๆ

=STDEV.P(range)   // ใช้กับข้อมูลที่มาจาก Population ทั้งหมด
=STDEV.S(range)   //ใช้กับข้อมูลที่มาจาก Sample ด้วยเหตุผลเดียวกับ VAR.S

Percentile

คือการเรียงข้อมูลจากน้อยไปมาก แล้วแบ่งข้อมูลออกเป็น 100 ส่วน สมมติว่าเราสอบได้คะแนน Percentile ที่ 83 หมายความว่า มีคน 83% ที่สอบได้คะแนนน้อยกว่าเรา

=PERCENTILE.INC(array, k)   // แบบ Inclusive หรือแบบที่เป็น =PERCENTILE เฉยๆ
=PERCENTILE.EXC(array, k)   // แบบ Exclusive

• แบบ Inclusive : อันดับโดย คำนวณจาก k*(N-1)+1 โดยที่ N คือจำนวนข้อมูล
• แบบ Exclusive : อันดับ คำนวณจาก k*(N+1) โดยที่ N คือจำนวนข้อมูล (นักสถิติมองว่าตัวนี้ตรงตามนิยามมากกว่า แต่มันจะมีปัญหากับ Percentile ที่ 0 กับ 100 ว่ามันจะ Error)

สำหรับคนที่สงสัยว่า Inclusive กับ Exclusive ต่างกันยังไง ลองดูคลิปที่ผมเคยทำไว้ได้ครับ

คลิปอธิบายความแตกต่างระหว่าง Inclusive กับ Exclusive

Quartile

คือการเรียงข้อมูลจากน้อยไปมาก แล้วแบ่งข้อมูลออกเป็น  4 ส่วน ถ้าเราอยู่ Quartile ที่ 3 แปลว่า มีข้อมูล 75% ที่น้อยกว่าเรา

=QUARTILE.INC(array,quart)  // แบบ Inclusive หรือแบบที่เป็น =QUARTILE เฉยๆ
=QUARTILE.EXC(array,quart)  // แบบ Exclusive

โดยที่

• Percentile ที่ 0 = Min (กรณี Inclusive)
• Q1 = Percentile ที่ 25
• Q2 = Percentile ที่ 50 = Median
• Q3 = Percentile ที่ 75
• Q4 = Percentile ที่ 100 = Max (กรณี Inclusive)

IQR (Interquartile Range)

คือการนำเอา Quartile 3- Quartile1

Box Plot หรือ Box and Whiskers Plot

เราสามารถเอาค่าพวก Mean และ Quartile มาแสดงเป็นกราฟที่เรียกว่า Box Plot ได้ ซึ่งเป็นกราฟที่สามารถแสดงการกระจายของข้อมูลได้ดีมากๆ อันดึงเลย แถมยังเหมาะกับการเปรียบเทียบการกระจายของข้อมูลหลายๆ กลุ่มได้ดีอีกด้วย

• เราเอาค่า Q1, Q2, Q3 มาสร้างเป็นตัวกล่อง (Box)
• คำนวณระยะมากสุดของแขนที่ยื่นออกมา (Whiskers) จาก Q1 และ Q3 ด้วยระยะทาง 1.5 เท่าของ IQR (บางที่อาจใช้ 3 เท่า)
• อย่างไรก็ตามถ้าค่า Min กับ Max ไม่เกินระยะมากสุดของแขนที่คำนวณ เราก็จะเอาแขนยื่นออกไปเท่ากับค่า Min, Max นะครับ
• ข้อมูลอะไรที่อยู่ไกลกว่าแขน Whiskers ที่ยื่นออกไป จะถูกมองว่าเป็น Outlier (ค่าที่น้อยหรือเยอะมากๆ เมื่อเทียบกับค่าอื่น) ซึ่งจะแสดงด้วยจุดแทนครับ
• และบางทีก็จะเอาค่า Mean มา Plot ด้วยเครื่องหมายกากบาทด้วย
• กราฟจะทำเป็นแนวนอนหรือแนวตั้งก็ได้ แล้วแต่ความชอบ 555

ใน Excel version ใหม่ๆ เราก็สร้างกราฟแบบ Boxplot ได้ง่ายๆ เลยครับ โดยที่ Excel จะใช้ Quartile แบบ Exclusive มาสร้างกราฟนะครับ

ใน Data 1 จะเห็นว่าค่า Mean ที่ควรเป็นค่ากลางของข้อมูลมันดันเด้งออกมานอกกล่องด้วยซ้ำ (ช่างเป็นค่ากลางที่แย่จริงๆ 555) ผมเลยลองแก้ค่า 100 เป็น 10 จะเห็นว่าค่า Mean ที่เด้งออกไปนอกกล่องใน Data1 นั้นกลับเข้ามาในกล่องได้อย่างสวยงาม ซึ่งแสดงให้เห็นว่าถ้าเราไม่มีค่า Outlier มาดึง Mean แล้วล่ะก็ มันก็เป็นค่ากลางที่ดีใช้ได้เลยล่ะ (หรือจริงๆ เลข 100 ที่ได้มาเป็นเลขที่พิมพ์ผิดกันนะ)

และนี่คือการคำนวณพื้นฐานทางสถิติที่ควรจะรู้จักครับ เดี๋ยวในตอนหน้าเราจะมาดูเรื่องพื้นฐานของทุกสิ่งทุกอย่าง นั่นก็คือ “การนับและความน่าจะเป็น” กันครับ

สารบัญซีรีส์ Statistics

• Statistics with Excel ตอนที่ 1 : ค่าสถิติที่สำคัญ
• Statistics with Excel ตอนที่ 2 : ความน่าจะเป็น
• Statistics with Excel ตอนที่ 3 : Discrete Probability Distribution
• Statistics with Excel ตอนที่ 4 : Normal Distribution
• Statistics with Excel ตอนที่ 5 : Central Limit Theorem
• Statistics with Excel ตอนที่ 6 : Hypothesis Testing
• การพยากรณ์ยอดขายใน Excel ด้วย Forecast และผองเพื่อน
• ลองทำ Machine Learning ใน Excel เทคนิค K-Means Clustering แบบไม่ง้อ VBA
• การทำ Simulation ด้วย Excel