Statistics with Excel ตอนที่ 3 : Discrete Probability Distribution

ในตอนที่แล้วเราได้เรียนเกี่ยวกับเรื่องความน่าจะเป็นไปแล้ว ในตอนนี้เราจะมาพูดถึงเรื่องของ Probability Distribution หรือการแจกแจงความน่าจะเป็นกันครับ

Probability Distribution เป็นการทำให้เราเห็นภาพรวมถึงค่าของตัวแปรสุ่มที่เป็นไปได้ทั้งหมด และสามารถหาค่าความน่าจะเป็นของเหตุการณ์ที่เราสนใจได้อีกด้วย จึงถือได้ว่ามันเป็นหัวใจสำคัญของเรื่องสถิติเลยล่ะ

Probability Distribution สามารถแบ่งออกเป็น  2 ประเภทใหญ่ๆ คือ

1. Discrete Probability Distributions : การแจกแจงความน่าจะเป็นแบบที่เหตุการณ์ที่สนใจนั้นสามารถนับแยกเป็นชิ้นๆ ได้(ไม่ได้มีค่าต่อเนื่องกัน) จึงสามารถ Plot กราฟเป็นแท่งๆ ได้เลย เช่น ใช้แจกแจงความน่าจะเป็นที่ที่ข้อสอบ 10 ข้อแล้วถูกต้อง 0,1,2,3,… 10 ข้อ ซึ่งจะได้กราฟ 10 แท่ง เป็นต้น ดังนั้นเราจะสามารถอ่านความน่าจะเป็นของเหตุการณ์ที่สนใจจากค่าแกน Y ได้เลยง่ายๆ
2. Continuous Probability Distributions : การแจกแจงความน่าจะเป็นแบบที่เหตุการณ์ที่สนใจนั้นไม่สามารถนับเป็นชิ้นๆ ได้ เพราะเลขมีค่าต่อเนื่องกัน เช่น การแจกแจงของน้ำหนักของคนในบริษัท น้ำหนักมันอาจเป็น 63.43 kg แบบนี้ได้ ซึ่งเป็นค่าต่อเนื่อง ทำให้การอ่านความน่าจะเป็นของกราฟที่ Plot ออกมาต้องอ่านจาก “พื้นที่ใต้กราฟ” แทน

ในบทความนี้เราจะมาเรียนรู้เรื่อง Discrete Probability Distribution กันก่อนนะครับ

Discrete Probability Distributions

เป็นการแจกแจงความน่าจะเป็นที่นับเป็นชิ้นๆ ได้ (ไม่ได้มีความต่อเนื่องกันจนแยกเป็นชิ้นไม่ได้) ซึ่งการที่เราเข้าใจ Distribution แบบนี้แล้ว จะทำให้เข้าใจที่มาที่ไปของ Distribution แบบ Continuous ที่เกิดขึ้นมากที่สุดในโลกที่มีชื่อว่า Normal Distribution ได้ด้วย

การแจกแจงความน่าจะเป็นแบบ Discrete ที่ผมจะขอพูดถึงมี 3 อัน คือ Bernoulli Distribution, Binomial Distribution, และ Poisson Distribution

Bernoulli Distribution

• คือการแจกแจงความน่าจะเป็นที่มีผลลัพธ์ 2 แบบ คือ สำเร็จ (จริง) และ ล้มเหลว(เท็จ) โดยมีความน่าจะเป็นของความสำเร็จคือ P และล้มเหลวคือ (1-P)
• มีค่า Mean = E(X)=P
• มี Variance = var(X)= P*(1-P)

ตัวอย่าง การมั่วข้อสอบ 1 ข้อ (มี choice 4 อัน)

• Mean = โอกาสที่จะสำเร็จ = 1/4 = 0.25
• Variance = (0.25)*(1-0.25) = 0.25*0.75 = 0.1875

หมายเหตุ: Bernoulli Distribution ถือเป็นตัวพื้นฐานที่แทบใช้อะไรไม่ได้มากเพราะใช้ได้แค่กรณีมี Trial ครั้งเดียว แต่เดี๋ยวเราจะได้เรียนตัวถัดไปที่มีชื่อว่า Binomial Distribution ซึ่งใช้ได้กับกรณีที่มี Trial กี่ครั้งก็ได้ อันนี้สิเจ๋งจริง! (แปลว่าจริงๆ แล้ว Bernoulli Distribution ก็คือการใช้ Binomial Distribution แบบมี Trial 1 รอบนั่นเอง)

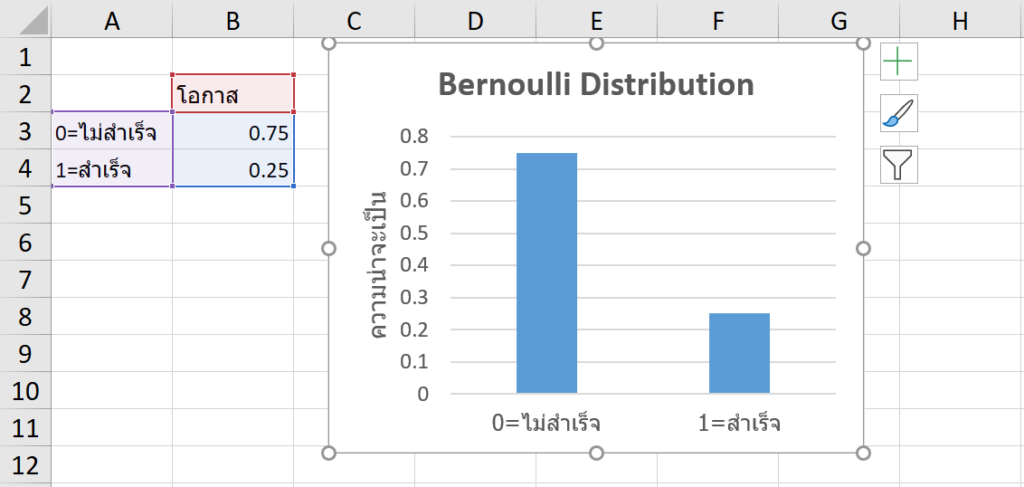
รูปการ Plot Bernoulli Distribution

เนื่องจากผลลัพธ์ของ Bernoulli Distribution เป็นไปได้แค่ 0=ไม่สำเร็จ, 1=สำเร็จ และมันมีแค่ Trial เดียว ดังนั้นผลลัพธ์ก็เลยมีแค่ 2 แท่งแบบ Basic ๆ นี่แหละ…

Binomial Distribution

• เป็นการทดสอบคล้ายๆ Bernoulli ก่อนหน้านี้ แต่คราวนี้โดยทำซ้ำๆ กัน n ครั้ง
• แต่ละครั้งมีผลลัพธ์ได้ 2 แบบ คือ สำเร็จ และ ล้มเหลว ความน่าจะเป็นของความสำเร็จ ในการทดลองแต่ละครั้งเท่ากัน คือ P
• การทดลองแต่ละครั้งเป็นอิสระต่อกัน (Independent) นั่นคือ ผลการทดลองครั้งต่อไปไม่ได้ขึ้นกับผลในครั้งก่อนหน้า
• ตัวอย่างเช่น มั่วข้อสอบ choice จำนวน 10 ข้อ แล้วดูว่าโอกาสถูก xx ข้อเป็นเท่าไหร่บ้าง

ดังนั้น Binomial Distribution เป็นการแจกแจงของจำนวนครั้งที่เกิดความสำเร็จ (X) ในการทดลอง Bernoulli trial ทั้งหมด n ครั้ง โดยมีความน่าจะเป็นของความสำเร็จคือ P

• มีค่า Mean คือ n*P
• มีค่า Variance คือ n * P * ( 1 – P )

เช่น มั่วข้อสอบ Choice จำนวน 10 ข้อ

• มีค่า Mean คือ n*P = 10 * 1/4 = 2.5
• มีค่า Variance คือ n * P * ( 1 – P ) = 10*1/4*3/4 = 1.875

การคำนวณ Binomial Probability หรือ ความน่าจะเป็นที่ความสำเร็จจำนวน X ครั้งจะเกิดขึ้น (ความน่าจะเป็นแต่ละแท่ง) มีสูตรดังนี้ 

b(x; n, P) = nCx * Px * (1 – P)n – x

สูตรดูเหมือนจะยุ่งๆ ยากๆ แต่จริงๆ แล้วที่มาที่ไปนั้น Make Sense ใช้ได้เลย เดี๋ยวมาดูการแทนค่ากันก่อน แล้วผมจะอธิบายที่มาของสูตรทีหลังนะครับ

ตัวอย่าง 1 : สมมติว่ามั่วข้อสอบ 10 ข้อ โอกาสที่ตอบถูก 6 ข้อพอดีคือเท่าไหร่?

• มีการทดลอง 10 ครั้ง n= 10
• จำนวนครั้งที่สำเร็จ X=6
• โอกาสที่จะสำเร็จได้แต่ละครั้ง = P = 1/4
• โอกาสที่ตอบถูก 6 ข้อพอดี = ₁₀C₆ * (1/4)^⁶ * (3/4)^⁴
• โอกาสที่ตอบถูก 6 ข้อพอดี = 0.016222 = 1.62%

ซึ่งที่มาที่ไปของสูตร จริงๆ ก็มาจากเนื้อหาตอนที่แล้วนี่แหละ

จากสูตรนี้ ₁₀C₆ * (1/4)^⁶ * (3/4)^⁴ เดี๋ยวเรามาดูกันว่าที่มาที่ไปแต่ละตัวมาจากไหน

• ทำข้อสอบ 10 ข้อ ตอบถูก 6 ข้อ แปลว่ามี 10 ขั้นตอน แล้วทำสำเร็จ 6 ขั้นตอน ไม่สำเร็จ 4 ขั้นตอน
• ในครั้งที่สำเร็จ จำนวน 6 ครั้งนั้น แต่ละอันมีโอกาส 1/4 ดังนั้นโอกาสจะเป็น 1/4 คูณกัน 6 รอบ หรือ (1/4)^⁶
• ในครั้งที่ไม่สำเร็จ จำนวน 4 ครั้งนั้น แต่ละอันมีโอกาส 3/4 ดังนั้นโอกาสจะเป็น 3/4 คูณกัน 4 รอบ หรือ (3/4)^⁴
• มีรูปแบบ Pattern ทั้งหมด เหมือนการสลับเพื่อสร้างคำใหม่จาก S6ตัวF4 ตัว = 10!/6!4! = ₁₀C₆
• Action ต้องทำต่อเนื่องกันดังนั้นก็เลยต้องเอาทุกตัวมาคูณกันทั้งหมด ก็เลยได้ว่า =₁₀C₆ * (1/4)^⁶ * (3/4)^⁴

แต่เรามี Excel ให้ใช้ ดังนั้นเราไม่ต้องมานั่งเขียนสูตรยากๆ เลย แต่ใช้ฟังก์ชัน BINOM.DIST ก็จะง่ายกว่ามากๆ 555

=BINOM.DIST(number_s,trials,probability_s,cumulative)
โดยที่ cumulative ถ้าเป็น TRUE คือโอกาสสะสมตั้งแต่ success เป็น 0 จนถึงจำนวนที่ต้องการ
โดยที่ cumulative ถ้าเป็น FALSE คือค่าโอกาสของจำนวน success ที่ต้องการตัวเดียว (ไม่สะสม)

ในที่นี่เราต้องการหาโอกาสที่ตอบถูก 6 ข้อพอดี ต้องใช้ cumulative ถ้าเป็น FALSE เพราะว่าไม่สะสม

=BINOM.DIST(6,10,1/4,FALSE) = 0.016222 = 1.62%

ตัวอย่าง 2 : สมมติเปลี่ยนคำถามเป็น ว่ามั่วข้อสอบ 10 ข้อ โอกาสที่ตอบถูกตั้งแต่ 6 ข้อขึ้นไป คือ เท่าไหร่?

แบบนี้คิดได้ 2 วิธี คือ เอาความน่าจะเป็นของถูก 6, 7, 8, 9, 10 ข้อ บวกกันให้หมด

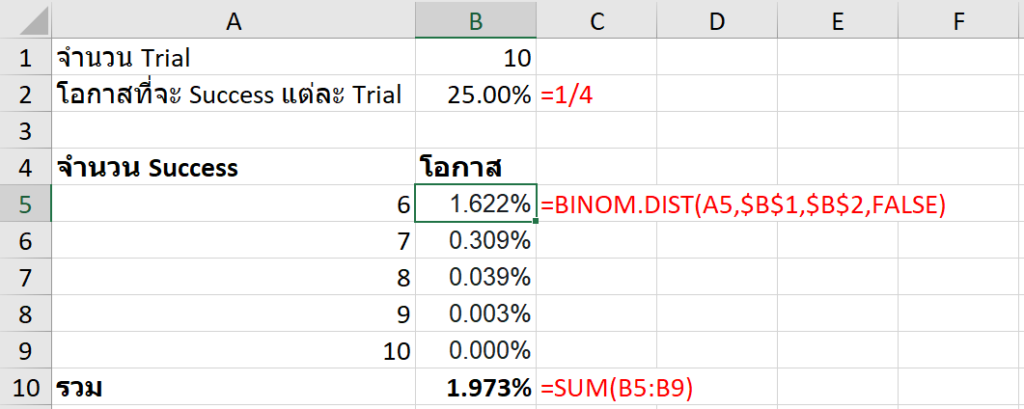
ซึ่งจะเห็นว่าต้องคำนวณเยอะ เรามาใช้อีกวิธีนั่นคือ การคิดในมุมกลับด้วยหลักการ Complement จะง่ายกว่าเยอะ

นั่นคือเอา 1- ความน่าจะเป็นสะสมจนถึง 5 ข้อ โดยที่เราจะเขียนเป็น 6-1 จะได้รู้ว่า 5 มาจากไหน และเราจะใช้ Cumulative เป็น TRUE

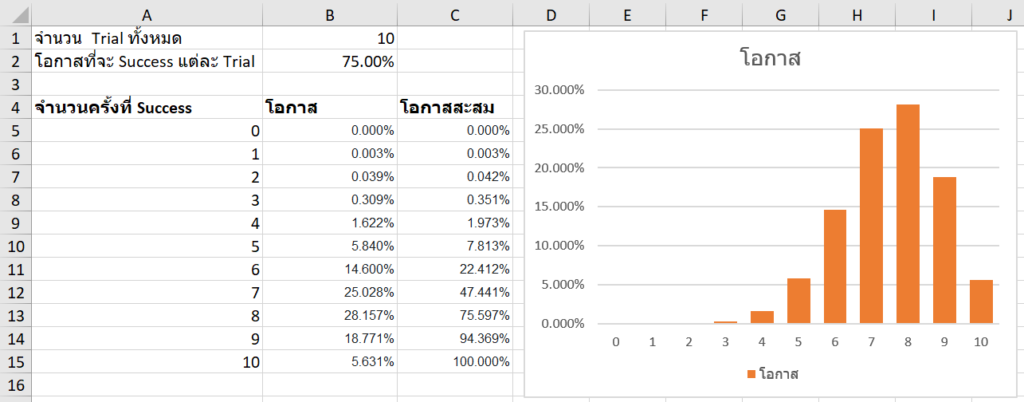
=1 - BINOM.DIST(6-1,10,1/4,TRUE) = 0.01973 = 1.973% เท่ากันเลยแต่ใช้สูตรช่องเดียว

รูปการ Plot Binomial Distribution

ที่โอกาสสำเร็จ 25% จะเห็นว่ากราฟค่อนข้างเบี้ยวๆ (รูปนี้เรียกว่าเบ้ขวา เพราะมีหางยาวไปด้านขวา)

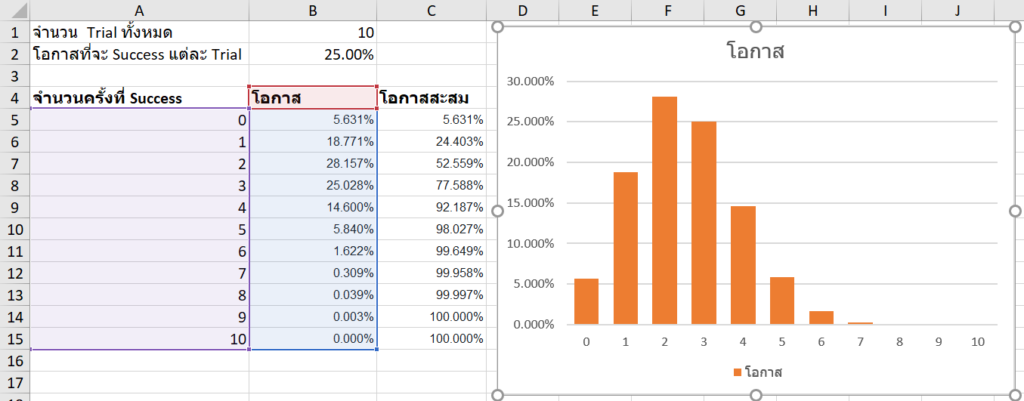
แต่ถ้าโอกาส Success เป็น 50% จะทำให้ Shape สมมาตรเลย

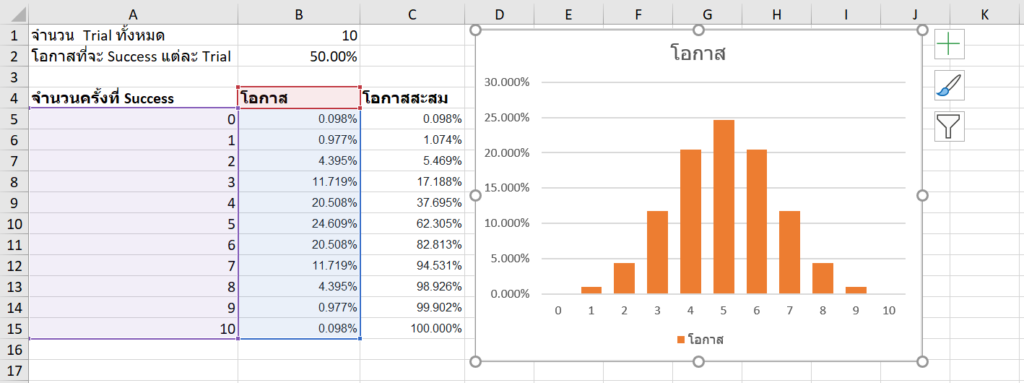
เช่น โอกาส Success เป็น 75% จะทำให้ Shape เบ้ไปอีกทิศ (เรียกว่าเบ้ซ้าย เพราะหางยาวไปด้านซ้าย)

Poisson Distribution

เป็นการแจกแจงจำนวนครั้งของความสำเร็จที่เกิดขึ้น (X) ภายในขอบเขตหรือระยะเวลาที่กำหนด โดยมีจำนวนครั้งของความสำเร็จโดยเฉลี่ยภายในขอบเขตหรือระยะเวลาที่กำหนดดังกล่าว เท่ากับ μ (จริงๆ จะเอาสัญลักษณ์อะไรก็ได้นั่นแหละ)

• มี Mean = μ
• มี Variance = μ (เท่ากับ Mean)

Poisson Probability หรือความน่าจะเป็นที่จะเกิดความสำเร็จ x ครั้งเป๊ะๆ ในเวลาที่กำหนดมีดังนี้ 

P(x; μ) = (e-μ) (μx) / x!

เช่น ปกติโดยเฉลี่ยแล้วบริษัทจะขายรถได้ 2 คัน ภายใน 1 วัน ถามว่าความน่าจะเป็นที่จะขายรถได้ 3 คันเป๊ะๆ ในวันพรุ่งนี้เป็นเท่าไหร่?

P(x; μ) = (e^^-μ) (μ^^x) / x!
P(3; 2) = (2.71828^^-2) (2^³) / 3!
P(3; 2) = (0.13534) (8) / 6
P(3; 2) = 0.1804 หรือ 18% นั่นเอง

ซึ่งใน Excel เราสามารถใช้ฟังก์ชัน POISSON.DIST ได้เลย

=POISSON.DIST(x,mean,cumulative) 

โดยที่ x คือจำนวนความสำเร็จที่ต้องการ mean คือ จำนวนความสำเร็จเฉลี่ย cumulative ถ้าเป็น TRUE คือโอกาสสะสมตั้งแต่ success เป็น 0 จนถึงจำนวนที่ต้องการ cumulative ถ้าเป็น FALSE คือค่าโอกาสของจำนวน success ที่ต้องการตัวเดียว (ไม่สะสม)

ดังนั้นข้อนี้ โอกาสจะขายรถได้ 3 คันเป๊ะภายใน 1 วันจะสามารถใช้สูตรได้ว่า

=POISSON.DIST(3,2,FALSE)  = 0.1804 หรือ 18% นั่นเอง

ถ้าข้อนี้ถามว่าโอกาสขายได้ตั้งแต่ 3 คันขึ้นไปภายใน 1 วันจะสามารถใช้สูตรได้ว่า

=1 - โอกาสสะสมที่ขายได้แค่ 2 คัน
=1 - POISSON.DIST(3-1,2,FALSE)
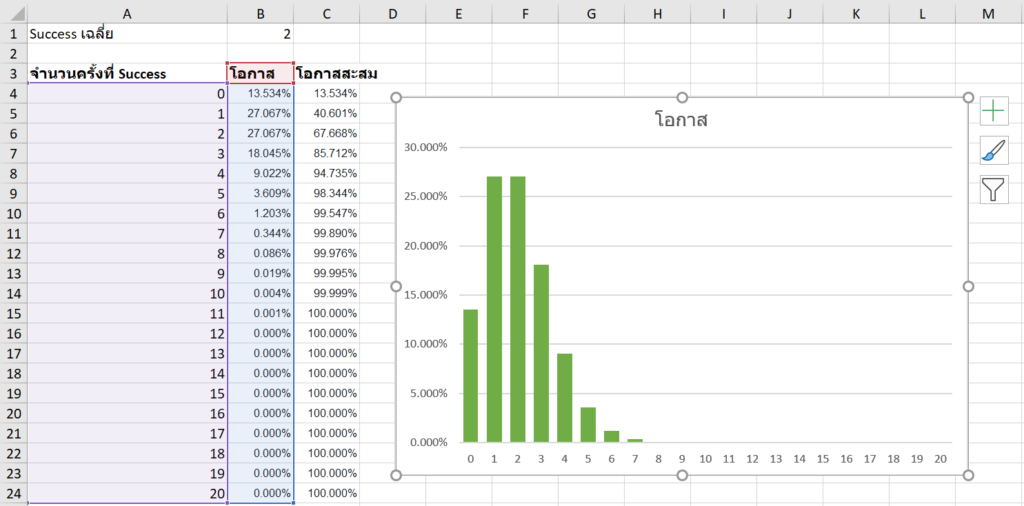
=0.72933 = 72.93%

รูปการ Plot Poisson Distribution

กรณี Success เฉลี่ยคือ 2

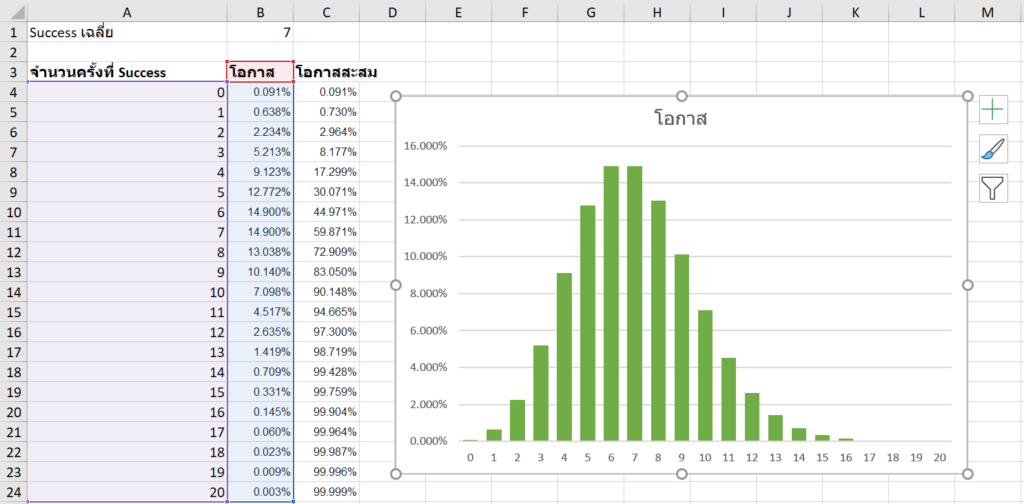
กรณี Success เฉลี่ยคือ 7

กรณี Success เฉลี่ยคือ 14

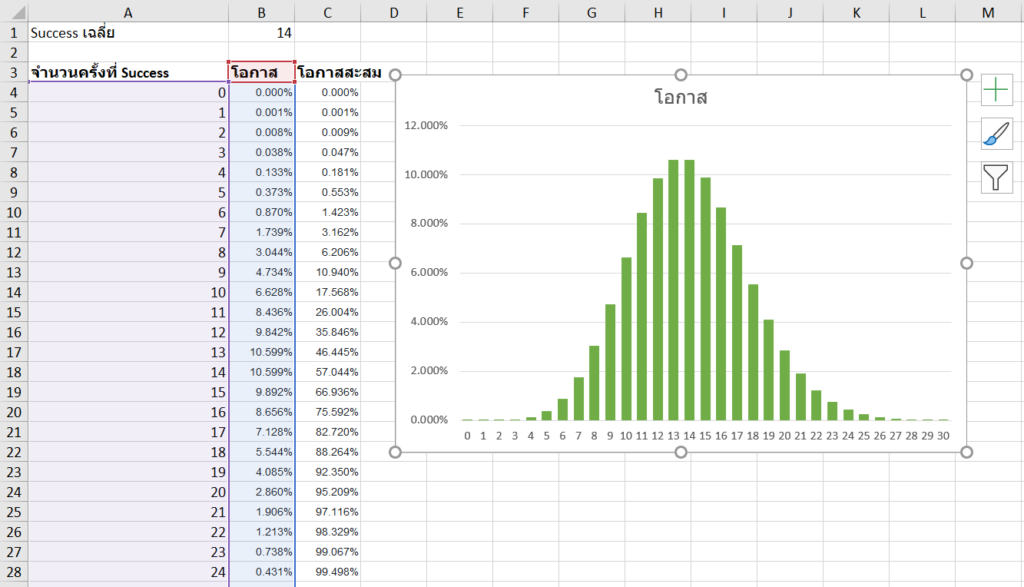
จะเห็นว่า Distribution จะเด้งสูงขึ้นมาที่ค่า Mean แล้วแผ่ออกไปทั้ง 2 ด้าน เป็นเหมือนภูเขา ยกเว้นว่าค่า Mean จะน้อยๆ ฝั่งซ้ายก็จะไปตันที่เลข 0 นั่นเอง

เอาล่ะสำหรับ Discrete Probability Distribution ที่ควรรู้จักก็ประมาณนี้แหละครับ หวังว่าจะเป็นประโยชน์สำหรับทุกท่านนะ

ตอนต่อไป

ในตอนต่อไปเราจะมาเรียนรู้เรื่องของ Continuous Probability Distributions ที่พบมากที่สุดในธรรมชาตินั่นก็คือ Normal Distribution นั่นเองครับ

สารบัญซีรีส์ Statistics