ทฤษฎีสุดเจ๋งอย่าง Central Limit Theorem นั้นเป็นสิ่งที่มีประโยชน์มากในการประมาณค่า Parameter ของ Population ได้จากการคำนวณค่า Statistic ของ Sample ครับ ดังนั้นเพื่อไม่ให้เสียเวลา เราไปดูกันเลย!
ตัวอย่างเช่น ถ้าผมต้องการทำการสำรวจส่วนสูงของคนในบริษัท แต่ผมไปสำรวจเก็บข้อมูลทุกคนมาไม่ไหว ก็เลยใช้วิธีเลือกสุ่มมาจำนวน 100 คนแล้วหาค่าเฉลี่ยของส่วนสูง ได้ 165 cm
- Population คือ คนในบริษัททั้งหมด
- Sample คือ คนในบริษัทที่ผมสุ่มมา 100 คน
- Parameter = เช่น ค่าเฉลี่ยของส่วนสูงของคนในบริษัททั้งหมด ( µ = ไม่รู้)
- Statistic = เช่น ค่าเฉลี่ยของส่วนสูงของคนในบริษัทที่ผมสุ่มมา 100 คน = xบาร์ = ได้ 165 cm
คำถามคือแล้วไอ้ 165cm ที่ผมได้นั้นมันจะใกล้เคียงกับค่า µ แค่ไหน?? และถ้าสุ่มมา 100 คนอีกที จะเฉลี่ยได้เท่าเดิมหรือไม่?? (แน่นอนว่าไม่) และไอ้เจ้า Mean (xบาร์) ของตัวอย่างที่สุ่มมาก็ดูจะไม่ค่อยมีความแน่นอนด้วย แล้วเราจะคิดยังไงต่อไปดีล่ะ?
โชคดีที่มันมีทฤษฎีที่ช่วยเราตอบได้ครับ ทฤษฎีนี้ชื่อว่า Central Limit Theorem (CLT) ซึ่งเป็นอะไรที่เจ๋งมากๆ เลย
Central Limit Theorem (CLT) สำหรับ Mean
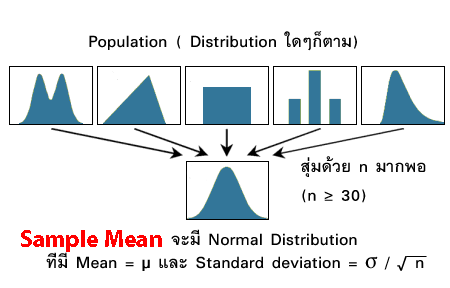
ทฤษฎีนี้บอกว่า ถ้าเราสุ่มตัวอย่างจาก Population (ที่มี distribution แบบไหนก็ได้ !!) ที่มีค่า Mean = µ และมีค่า Standard deviation = σ แล้วล่ะก็
เมื่อมีการสุ่มตัวอย่างในอุดมคติ ที่สุ่มแล้วมีการใส่คืน* ด้วย sample size ที่ใหญ่มากพอ (จะให้ดี n ต้อง ≥ 30** ) การแจกแจงความน่าจะเป็นของ xบาร์ของตัวอย่างที่สุ่มมา (Distribution of Sample Mean) จะสามารถอธิบายได้ด้วย Normal Distribution
- มี Mean = µ (แปลว่า distribution นี้จะมี mean เท่ากับ population จริง)
- Standard deviation = σ / √ n (แปลว่า distribution นี้จะมี sd น้อยกว่า population จริง
- เราจะเรียก Standard deviation ของ การแจกแจง Sample Mean หรือเจ้า σ / √ n ว่า Standard Error of Estimates หรือ SE (estimate) ซึ่งผมอาจจะใช้คำสั้นๆ ว่า Standard Error หรือ SE นะครับ
- ย้ำว่า ไม่ใช่การแจกแจงของ item ในตัวอย่างแต่ละชุดนะครับ แต่เป็นการแจกแจงของ xบาร์ของตัวอย่างที่เป็นไปได้ทั้งหมดจากทุกๆ trial (Distribution of Sample Mean) ถ้าใครงงเดี๋ยวดูตัวอย่างในหัวข้อ Simulation ได้ครับ
* ถ้าสุ่มในชีวิตจริงมันใส่คืนไม่ได้อยู่แล้ว ขอให้สุ่มมาไม่เกิน 5-10% ของ population ละกัน เพื่อจะได้ให้แต่ละ sample นั้น independent กัน จะได้ไม่ bias จนเกินไป เพราะสูตร Standard deviation จริงๆ ต้องเป็น ( σ / √ n )* SQRT( (N-n)/(N-1) ) แต่ถ้า n (จำนวน sample) น้อยมากๆ เมื่อเทียบกับ N (จำนวน Population) จะทำให้ SQRT( (N-n)/(N-1) ที่เรียกว่า Finite Population Correction Factor มีค่าเป็น 1 ทำให้ Standard deviation = σ / √ n ง่ายๆ ได้เลย
** อย่างไรก็ตามถ้า Population มี Distribution แบบ Normal อยู่แล้ว ถึงจะสุ่ม Sample จำนวนน้อยกว่า 30 ก็ยังจะได้ออกมาเป็น Normal Distribution อยู่ดีครับ แต่ถ้า distribution ของ population เบ้หนักมากๆ n อาจต้อง ≥ 50 จะปลอดภัยกว่า
นั่นคือ
xบาร์ ~ Normal (µ, σ / √ n )ถ้าแปลงเป็น standard normal distribution แบบบทที่แล้ว จะได้ว่า
z = (xบาร์ – µ) / (σ / √ n) ~ Normal (0,1)ลองทดสอบ CLT ดูด้วย Simulation ใน Excel
ผมจะสุ่มค่าจากเลข Random 0-1000 ออกมาด้วย RAND()*1000 เราได้เรียนรู้ไปในตอนที่แล้วว่ามันเป็น Uniform Distribution (ซึ่งเป็นรูปสี่เหลี่ยมผืนผ้าโง่ๆ เลยนะ ไม่มีความคล้าย Normal ด้วยซ้ำจริงมะ )โดยสุ่มออกมาครั้งละ 50 ตัว จากนั้นหาค่า Mean ซึ่งถ้ากด F9 เลขที่ได้จะเปลี่ยนไปเรื่อยๆ จากการ Random
ตัวนี้เราแอบรู้อยู่แล้วว่า Uniform Distribution มี population mean และ sd ดังนี้
- Mean = ค่าเฉลี่ยตรงกลาง = (a+b)/2 = (0+1000)/2 =500
- Variance = 1/12 * (b-a)^2
- σ= SQRT(Variance) = SQRT(1/12 * (1000-0)^2) = 288.675
แต่เราจะทำเป็นไม่รู้ก่อนว่าค่าจริงเป็นยังไง แต่จะลองดูว่าที่สุ่มมาจะประมาณค่าจริงได้แม่นแค่ไหน
สุ่มครั้งแรก
สุ่มครั้งที่ 2 : โดยกด F9 เพื่อสุ่มใหม่ ค่าที่ได้ก็จะเปลี่ยนไป
เราจะทำ Simulation เหตุการณ์แบบนี้ 100 ที (สุ่ม 100 รอบ) ใน Excel แล้วนำค่า Mean ที่ได้มา Plot Distribution ดูสิว่าจะออกมาเป็นยังไง?
เทคนิคการทำ Simulation ใน Excel ที่เป็นที่นิยม คือใช้ Data -> What if Analysis -> Data Table มาช่วย ดังนี้ (เลขจะเปลี่ยนไปมาก็ช่างมัน)
2.เลือกคลุมพื้นที่ H4:I104
3. เรียกใช้เครื่องมือ Data -> What if Analysis -> Data Table
4. เลือก Column Input Cell เป็นช่องว่างๆ ช่องไหนก็ได้
5. กด ok
ผลลัพธ์ที่ออกมาจะได้ค่าที่ผ่านวิธีการแบบเดียวกับ I4 ออกมาอีก 100 ช่อง (แต่ random เลขเลยเปลี่ยนไป)
ถ้าเรานำ Data ใน I5:I104 มา Plot Histogram จะได้ดังรูป ซึ่งดูใกล้เคียงกับกราฟ Normal หรือ t-distribution ใช้ได้เลย
และจะเห็นว่า
- ค่าเฉลี่ยของ Sample Mean =AVERAGE(I5:I104) = 499.2247 ซึ่งใกล้เคียงกับ Mean Population จริงซึ่งก็คือ 500 มากๆ
- ค่า SE (estimate) =46.61 ซึ่งจาก CLT ควรจะประมาณ σ / √ n = 288.675/SQRT(50) = 40.82 ซึ่งก็ถือว่าใกล้เคียงล่ะ
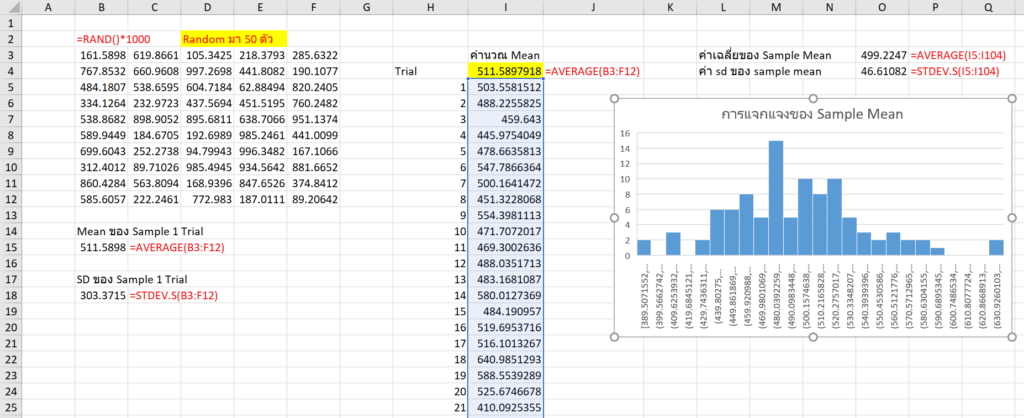
จะเห็นว่ายิ่งเราทำ Simulation จำนวน trial เยอะๆ เช่น 1000 ครั้ง แล้วเอามาทำ Distribution จะได้การแจกแจงของ Sample Mean ที่สวยเป็น Normal มากขึ้น และมี Mean ของ Sample Mean และ SE (estimate) ที่แม่นตรงกับทฤษฎี CLT มากขึ้นไปอีก
ถ้าเราไม่รู้ standard deviation ของ population ล่ะ?
แต่ถ้าหากเรายังไม่รู้ standard deviation ของ population อีกจะทำยังไงดี? (ซึ่งในชีวิตจริงไม่รู้หรอก ถ้ารู้แล้วจะสุ่ม sample ทำไมฟะ)
คำตอบก็คือ ใน SE (estimate) ให้เราสามารถแทน σ ด้วย s (standard deviation ของ sample) ที่เราสุ่มได้เลย เพียงแต่มันจะเปลี่ยน distribution จาก Normal Distribution เป็น t-distribution ที่มี degree of freedom = n-1 แทน (จำนวน sample size -1)
t-Distribution
ลักษณะของ t distribution นั้น หน้าตาคล้ายๆ กับ Normal Distribution มีลักษณะสมมาตร ที่ mean =0 เช่นกัน
ซึ่ง degree of freedom (df) คืออะไร ช่างมันไปก่อนนะ เอาเป็นว่า
- ถ้า df น้อยๆ shape ของ t-distribution จะบานออกและเตี้ยลง
- ถ้า df เยอะๆ shape ของ t-distribution จะผอมลง สูงขึ้น จนเริ่มคล้ายกับ standard normal distribution มากขึ้น
การใช้ t-distribution นั้นมีประโยชน์ตรงที่เราไม่จำเป็นต้องรู้ standard deviation ของ population ก็ได้ และยังสามารถใช้กับ sample size น้อยๆได้ด้วย เพียงแต่ว่า หาก sample มาจาก population ที่ไม่ได้เป็น normal ก็ควรจะมี sample size ≥ 30 จึงจะแม่นยำ
นั่นคือ จาก (xบาร์ – µ) / (σ / √ n) ~ N (0,1) จะกลายเป็น
(xบาร์ – µ) / (s / √ n) ~ t (df=n-1)ดังนั้น SE (estimate) ของ t-distribution จะเป็น s / √ n แทน
ตัวอย่างของการใช้ฟังก์ชัน T.DIST ทั้งหลาย จะมี 3 แบบ คือ แบบ Left Tail, 2Tails, Right Tail เป็นดังนี้
สรุปการใช้ Central Limit Theorem กับค่า Sample Mean
- เมื่อใดก็ตามที่เรารู้ σ ของ population ก็สามารถใช้ Normal Distribution ได้
- xบาร์ ~ Normal (µ, σ / √ n )
- เมื่อใดก็ตามที่เราไม่รู้ σ ของ population ก็สามารถใช้ sd ของ sample ใน SE (estimate) โดยใช้ t-Distribution ได้
- xบาร์ ~ t (µ, s / √ n, df=n-1)
- ย้ำว่า s คือ standard deviation ของ sample ของเรา (ไม่ใช่ sd ของ sample mean นะ)
ซึ่งสถานการณ์ที่เราใช้ t-distribution แทน normal ก็คือ ใช้กับกรณีที่เราไม่รู้ทั้ง µ และ σ ของ population เราเลยใช้ s (standard deviation ของ sample) แทน σ ไป และใช้ t-distribution ที่มี Shape อ้วนกว่า Normal ปกติมาดัก error นั่นเอง แต่ถ้าเราไม่รู้ µ อย่างเดียว เราก็ใช้ Normal Distribution ได้ครับ
แล้วจะรู้ได้ไงว่าการสุ่ม 1 Trial ของเรานั่นแม่นยำแค่ไหน?
เนื่องจากเวลาเราสุ่ม sample ออกมาแล้วหาค่า Mean กับ Sd มันอาจจะไม่ตรงกับ Parameter จริงๆของ population ก็ได้ และอาจห่างกันได้มากด้วย เช่น
- สุ่มครั้งแรก ได้ Mean 517.2163, SD = 259.1704
- สุ่มครั้งสอง ได้ Mean 483.0414, SD = 311.7958
- แต่ค่า Population จริง Mean = 500, SD = 288.675 (แต่เราทำเป็นไม่รู้ไปก่อน)
มันจึงควรมีการบอกว่า จากการสุ่ม 1 ทีของเราแล้วได้ค่า Mean มา จะสามารถประมาณการค่าของ Parameter จริงเป็นเท่าไหร่ โดยจะต้องบอกด้วยว่ามีความแม่นยำแค่ไหน และนั่นก็คือที่มีของคำศัพท์ว่า Confidence Level และ Confidence Interval นั่นเอง
Confidence Level และ Confidence Interval
เราจะบอกได้ว่า ด้วยระดับความมั่นใจ (Confidence Level) เท่านี้เปอร์เซ็นต์ ค่า Parameter จริงๆ ของ population น่าจะตกอยู่ในช่วงไหนถึงไหน (Confidence Interval)
มาดูแนวคิดของเรื่องนี้กันนะครับ สมมติว่า Distribution เป็น Normal Distribution ก่อนจะได้ไม่งง จากความรู้เรื่อง Standard Normal Distribution เราจะรู้ว่า
z = (x - Mean) / sdซึ่งในกรณี distribution ของ sample mean จะได้ว่า
- x = sample mean ที่เราสนใจ
- mean = µ ของ population
- sd = SE (estimate)
ดังนั้นค่า z จะได้ว่า
z = ( sample mean - µ ) / SE (estimate)และรู้ว่าสำหรับ standard normal distriution ค่า mean ± 1.96 จะกินพื้นที่ 95% ของส่วนกลางของ distribution (ซึ่งmean คือ 0)
นั่นคือ ( sample mean – µ ) / SE (estimate) = 0 ± 1.96
ซึ่งพอย้ายข้างจะได้ว่า
- Sample mean – µ = ± 1.96 * SE (estimate)
- สลับย้ายค่า µ ให้อยู่ซ้ายสุดตัวเดียว จะได้ว่า
- µ = Sample mean ± 1.96 * SE (estimate) นั่นเอง ที่ความมั่นใจ 95%
ดังนั้นเราเลยสามารถสรุปสูตรทั่วๆไปของช่วงที่ µ จะอยู่ ซึ่งเรียกว่า Confidence Interval คือ
Confidence Interval = sample mean ± multiplier x SE (estimate)
- multiplier จะขึ้นอยู่กับ Confidence Level (ระดับความมั่นใจ) ยิ่งระดับมั่นใจมาก multiplier ก็จะยิ่งมาก (ทำให้กินช่วงกว้างขึ้น) ซึ่งก็ขึ้นอยู่กับว่าใช้ Normal Distribution หรือ t-distribution ด้วยนั่นเอง ซึ่ง 1.96 มาจาก 95% ของ Standard Normal
- ค่า multiplier แบบเป๊ะๆ สามารถใช้ฟังก์ชันกลุ่ม INVERSE ของแต่ละ Distribution มาช่วยคำนวณหาได้ (จะแสดงให้ดูในตัวอย่างถัดไป)
- SE (estimate) ก็คือค่า (σ / √ n) ถ้ารู้ σ ของ population หรือ (s / √ n) ถ้าไม่รู้ σ ของ population (ซึ่งต้องใช้ t-distribution ไปด้วย)
กลับมายังโจทย์ที่เรา Random เลข 0-1000
ลองหา confidence interval ที่ความมั่นใจระดับ 95% จากข้อมูลในรูปแรก (Mean 517.2163, SD = 259.1704)
Confidence Interval = Sample Mean ± multiplier x SE (estimate)ถ้าเรารู้ σ ของ population
ก็สามารถใช้ normal distribution ได้นะ ดังนั้นจะได้ว่า
Confidence Interval ของ µ = Sample Mean ± z.multiplier x σ / √ n- Sample Mean = 517.2163
- σ = population standard deviation = 288.675
- n = 50 เพราะสุ่มมา 50 ตัว
- z-Distribution ความมั่นใจ 95% อยากรู้ว่า z.multiplier มีค่าเท่าไหร่ สามารถใช้ NORM.S.INV มาช่วยได้
- เนื่องจาก NORM.S.INV นับพื้นที่จากฝั่งซ้าย การจะได้ความเชื่อมั่น 95% จะต้องนับจากขอบซ้ายมา 2.5%
- =NORM.S.INV(2.5%)
- =-1.959963985
- = จะได้ว่า z-multiplier ก็คือ 1.96 ตามที่เคยเรียนมาสมัยเด็กๆนั่นเอง
Confidence Interval ที่ 95% = 517.2163 ± 1.96 * 288.675 / SQRT(50)
- ขอบล่าง = 517.2163 – 1.96 * 288.675 / SQRT(50) = 437.20
- ขอบบน = 517.2163 + 1.96 * 288.675 / SQRT(50) = 597.23
ดังนั้น µ ของ Population จะอยู่ในช่วง 437.20 – 597.23 ด้วยความมั่นใจ 95% นั่นเอง
ถ้าเราไม่รู้ σ ของ population
ก็ต้องใช้ t-distribution นะ ดังนั้นจะได้ว่า
Confidence Interval ของ µ = Sample Mean ± t.multiplier x s / √ n- Sample Mean = 517.2163
- s = sample standard deviation = 259.1704
- n = 50 เพราะสุ่มมา 50 ตัว
- t-Distribution ความมั่นใจ 95% อยากรู้ว่า t.multiplier มีค่าเท่าไหร่ สามารถหาได้ 2 วิธี
- ใช้ T.INV มาช่วยได้
- เนื่องจาก T.INV นับพื้นที่จากฝั่งซ้าย การจะได้ความเชื่อมั่น 95% จะต้องนับจากขอบซ้ายมา 2.5%
- =T.INV(probability,deg_freedom)
- =T.INV(2.5%,50-1) = -2.009
- ใช้ T.INV.2T มาช่วย
- เนื่องจาก 2T นับพื้นที่จากขอบทั้งสองฝั่ง การจะได้ความเชื่อมั่น 95% จะต้องนับจากขอบมา 2 ฝั่งรวมกันให้ได้ 5%
- =T.INV.2T(probability,deg_freedom)
- =T.INV.2T(5%,50-1) = 2.009
- สรุปแล้วจะได้ว่า t-multiplier ก็คือ 2.00 นั่นเอง (ซึ่งจะกว้างกว่า 1.96 กรณีเป็น normal)
- ใช้ T.INV มาช่วยได้
Confidence Interval ที่ 95% = 517.2163 ± 2.00 * 259.1704 / SQRT(50)- ขอบล่าง = 517.2163 – 2.00 * 259.1704 / SQRT(50) = 443.912
- ขอบบน = 517.2163 + 2.00 * 259.1704 / SQRT(50) = 590.521
ดังนั้น µ ของ Population จะอยู่ในช่วง 443.912 – 590.521 ด้วยความมั่นใจ 95% นั่นเอง
ซึ่งทั้ง 2 กรณีมันก็เดาถูกนะ เพราะจริงๆ Population Mean ของ Uniform Distribution = AVERAGE(0,1000) = 500 นั่นเอง
อย่างไรก็ตาม เนื่องจากนี่คือระดับความมั่นใจ 95% แปลว่ามีโอกาส 5% ที่ population mean ไม่ได้อยู่ในช่วงที่เราคิดนะครับ
เช่น ผมดันซวย Sampling ได้แบบนี้
Confidence Interval ของ µ = Sample Mean ± t.multiplier x s / √ n
Confidence Interval ที่ 95% = 587.8903 ± 2.00 * 292.2328 / SQRT(50)
Confidence Interval ที่ 95% = 505.23 - 670.54 ซึ่ง เลข 500 ไม่ได้อยู่ในนี้การใช้ Central Limit Theorem กับค่า Proportion
ถ้าเรามีการเก็บข้อมูลที่มีลักษณะเป็นสัดส่วน (proportion หรือ P) เราก็ยังสามารถใช้ CLT มาประยุกต์ได้ครับ แถมง่ายกว่าปกติด้วย ซึ่งข้อมูลที่เป็น Proportion นั้นแปลว่าตัวอย่างแต่ละตัวที่สุ่มมานั้นมาจาก Population ที่มีการแจกแจงแบบ 0=no,1=yes หรือ Bernouilli distribution นั่นเอง
ซึ่งถ้าพอจำได้ Bernouilli distribution มีลักษณะดังนี้
- มีค่า Mean = E(X)=P
- มี Variance = var(X)= P*(1-P)
- ดังนั้นมี SD = SQRT( P*(1-P) )
ตัวอย่างเช่น ถ้าผมต้องการทำการสำรวจ Portion ของผู้ชายของคนในบริษัทที่มีพนักงาน 3000 คน แต่ผมไม่รู้ว่ามีพนักงานชายกี่ % ผมก็เลยสุ่มพนักงานมาจำนวน 100 คนแล้วเช็คแล้วได้ว่าเป็นชาย 45 คน
- Population คือ คนในบริษัททั้งหมดมีประมาณ 3000 คน
- Sample คือ คนในบริษัทที่ผมสุ่มมา 100 คน
- Parameter = เช่น สัดส่วนที่เป็นผู้ชายของคนในบริษัททั้งหมด ( P = ไม่รู้)
- Statistic = เช่น สัดส่วนที่เป็นผู้ชายของคนในบริษัทที่ผมสุ่มมา 100 คน =เรียกว่า p = ได้ 45/100 = 0.45
จากเดิมบอกว่า CLT จะให้ดี sample size n ต้อง ≥ 30 แต่พอมาใช้กับ proportion แล้ว จะมีเกณฑ์เปลี่ยนไปเล็กน้อยว่า
np ต้อง ≥ 10 และ n(1-p) ก็ต้อง ≥ 10 ด้วย จึงจะให้ผลที่ประมาณว่าเป็น Normal Distribution อยู่ (บางเกณฑ์ก็บอกว่าต้องมากกว่าหรือเท่ากับ 5 ก็พอใช้ได้แล้ว)
- ที่ต้องมี Condition ดักทั้งสองฝั่ง เพื่อไม่ให้ค่า p อยู่ใกล้ 0% หรือ 100% มากจนเกินไป (ถ้าเป็นงั้นกราฟจะเบ้จนไม่เป็น Normal)
- ยกเว้นว่าจะมีจำนวน n เยอะจนที่ให้ Standard Errorp หรือ SEp น้อยลง จนทำให้กราฟหายเบ้ได้
ใครอยากเห็นภาพมากขึ้นลองดูคลิปนี้ได้
เช่น ในตัวอย่าง
- np ต้อง ≥ 10 : 100*0.45 ต้อง >= 10 ซึ่งจริง เพราะได้ 45
- n(1-p) ต้อง ≥ 10 : 100*(1-0.45) ต้อง >= 10 ซึ่งจริง เพราะได้ 55
และจาก CLT จะได้ความสัมพันธ์ว่า sample proportion แจกแจงตาม Normal Distribution โดยมีลักษณะ
- มี Mean = P (แปลว่า distribution นี้จะมี mean เท่ากับ population จริง)
- Standard deviation = SE (estimate) = σ / √ n (แปลว่า distribution นี้จะมี sd น้อยกว่า population จริง)
- ค่า σ ของ Bernouilli distribution = SQRT( P*(1-P) )
- แปลว่า σ / √ n = SQRT( P*(1-P)/n )
แปลว่าเราจะรู้ว่า distribution ของ sample proportion จะแจกแจงแบบ Normal เสมอ โดยที่ไม่ต้องมีบางกรณีที่ต้องใช้ t-distribution เหมือนกับกรณี Sample Mean เลย (สาเหตุเพราะจริงๆ แล้วค่า σ ของ Bernouilli distribution มันคำนวณมาจากค่า Mean อยู่ดี แปลว่าจริงๆ แล้วเราไม่รู้ค่า Mean แค่ตัวเดียวเท่านั้น จึงถือว่าใช้ Normal Distribution ได้เสมอครับ)
p ~ N (P, SQRT( P*(1-P)/n )) Confidence Interval ของ Proportion
Confidence Interval = Sample Mean ± multiplier x SE (estimate)
จะกลายเป็น
Confidence Interval สำหรับ P = p ± z* SQRT( P*(1-P)/n )ค่า z* ก็ขึ้นอยู่กับระดับความมั่นใจเช่นเดิม เช่น 95% จะเป็น 1.96
จากตัวอย่างของเรา
- ค่า sample p = 45/100 = 0.45
- n = 100
- z เกิดจากการหา =NORM.S.INV(probability) ซึ่งเป็นแบบสะสมจากด้านซ้าย ถ้าอยากได้มั่นใจ 95% แปลว่า ด้านซ้ายต้องวิ่งมา 2.5% หรือไปขวาถึง 97.5% ก็ได้ว่า z=1.9599 หรือ 1.96 ที่เคยท่องมาตอนเด็กๆ นั่นเอง
- P ขอบล่าง = 0.45 – 1.96* SQRT(0.45 * ( 1 – 0.45 ) / 100) = 0.3525
- P ขอบบน = 0.45 + 1.96* SQRT(0.45 * ( 1 – 0.45 ) / 100) = 0.5475
ดังนั้น P ของ Population จะอยู่ในช่วง 0.3525 – 0.5475 ด้วยความมั่นใจ 95% นั่นเอง
โจทย์ตัวอย่าง : ทดสอบพลังหมัดนักสู้ฝีมือดี
สมมติว่าคุณต้องการนักสู้ฝีมือดีจำนวนมากจากบริษัทผลิตนักสู้แห่งหนึ่ง ซึ่งเราต้องการผลการ Test การวัดพลังหมัดของนักสู้ของบริษัทเค้าเป็นหลักฐานด้วยว่าโดยเฉลี่ยแล้วนักสู้ในกลุ่มควรมีพลังหมัด 690 ขึ้นไปจึงจะทำการว่าจ้างอย่างเป็นทางการ
ซึ่งเค้าอ้างว่า เค้าได้วัดพลังหมัดของนักสู้ของเค้าทุกคนจำนวน 1000 คน เรียบร้อยแล้วแต่ยังหาผลการ test ไม่เจอ ให้รอแปป…
ด้วยความที่เราเป็นคนใจร้อนและเชื่อคนยาก จึงได้ขอสุ่มนักสู้มา 60 คน แล้วปรากฏว่าวัดพลังหมัดเฉลี่ยได้แค่ 670 เท่านั้น โดยมี sd ของ sample = 55
เนื่องจากสุ่มมา 60 คน จึงเพียงพอที่จะใช้ CLT ได้ ดังนั้นมี 2 คำถาม คือ
มาเริ่มที่ข้อแรก : ประมาณการ Population จาก Sample
ให้ประมาณการค่าพลังหมัดของ Population จริง จากข้อมูลการสุ่มที่ได้ ด้วยความมั่นใจ 95%
เนื่องจาก ไม่รู้ข้อมูล µ กับ σ ของPopulation ดังนั้นต้องใช้ t-distribution แทน Normal
Confidence Interval ของ µ = Sample Mean ± t.multiplier x s / √ n
t.multiplier=T.INV.2T(5%,60-1)=2
Confidence Interval ของ µ = 670 ± 2 * 55/SQRT(60) ที่ความมั่นใจ 95%- ขอบล่าง µ = 670-2*55/SQRT(60) = 655.79
- ขอบบน µ = 670+2*55/SQRT(60) = 684.20
ดังนั้น µ หรือพลังหมดเฉลี่ยของนักสู้ทั้งหมด ควรอยู่ในช่วง 655.79-684.20 ที่ความมั่นใจ 95%
ต่อมาทางบริษัทบอกว่าเจอผลการทดสอบแล้ว โดยผลการวัดพลังหมัดโดยเฉลี่ยออกมาแล้วอยู่ที่ 700 และมี sd อยู่ที่ 50
ต่อด้วยข้อที่ 2 : หาความ Make Sense ของสิ่งที่ทางบริษัทเคลมมา
จงคำนวณว่ามีโอกาสแค่ไหนที่ค่าเฉลี่ยของ population อยู่ที่ 700 จริง แต่เราดัน sample มาได้ค่าเฉลี่ยน้อยกว่าหรือเท่ากับ 670
สมมติว่าที่บริษัทอ้างมาจริง คือ µ=700 และมี σ= อยู่ที่ 50 แปลว่าตอนนี้เรารู้ σ แล้ว ดังนั้นใช้ Normal Distribution ได้
การแจกแจงของ Sample Mean ควรจะเป็น Normal ที่มี Mean=700 และ sd คือ SE (estimate) = σ/√ n = 50/SQRT(60)
ถ้าเราอยากหาความน่าจะเป็นที่ดันลองสุ่มแล้วได้ค่าเฉลี่ยน้อยกว่าหรือเท่ากับ 670 ก็คือพื้นที่ฝั่งซ้าย ดังนั้นใช้ NORM.DIST ได้เลย
=NORM.DIST(x,mean,standard_dev,cumulative)
=NORM.DIST(670,700,50/SQRT(60),TRUE)
=0.000168%ซึ่งจะเห็นว่าแทบเป็นไปไม่ได้เลยที่เราจะโชคร้ายสุ่มได้ค่าที่ห่วยขนาดนี้ แปลว่าที่บริษัทนักสู้อ้างค่าเฉลี่ยมาดูจะสูงเกินจริงแล้วล่ะ ไม่ว่าจะมองจากมุมมองในคำตอบข้อแรก หรือมองในมุมมองของคำตอบข้อที่ 2 ก็ตาม
ตอนต่อไป
ตอนต่อไปจะเป็นเรื่องการทดสอบสมมติฐานที่เรียกว่า Hypothesis Testing แล้วครับ เป็นเรื่องที่เป็นหัวใจสำคัญของ Inferential Statistics เลยล่ะ ซึ่งเดี๋ยวคุณจะได้รู้จักกับคำว่า Significant กับคำว่า p-Value ซึ่งเป็นคำศัพท์ยอดฮิต (แต่หลายคนแปลไม่ออก) ซักที
สารบัญซีรีส์ Statistics
- Statistics with Excel ตอนที่ 1 : ค่าสถิติที่สำคัญ
- Statistics with Excel ตอนที่ 2 : ความน่าจะเป็น
- Statistics with Excel ตอนที่ 3 : Discrete Probability Distribution
- Statistics with Excel ตอนที่ 4 : Normal Distribution
- Statistics with Excel ตอนที่ 5 : Central Limit Theorem
- Statistics with Excel ตอนที่ 6 : Hypothesis Testing
- การพยากรณ์ยอดขายใน Excel ด้วย Forecast และผองเพื่อน
- ลองทำ Machine Learning ใน Excel เทคนิค K-Means Clustering แบบไม่ง้อ VBA
- การทำ Simulation ด้วย Excel
