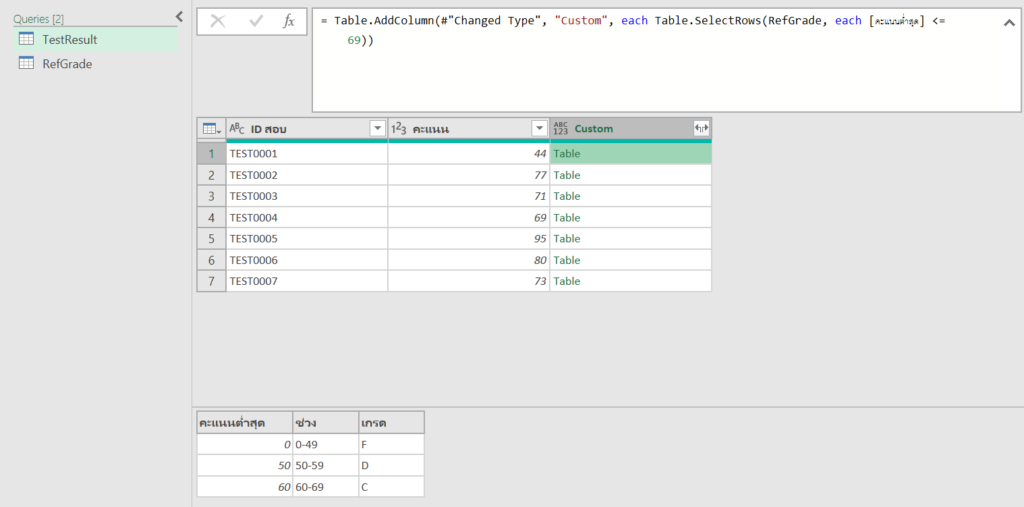
หลายครั้ง Excel แสดงอาการแปลกๆ ออกมาทำให้เรางง รู้หรือไม่เป็นเพราะว่าเรากำลังเจอกับกับดักอยู่โดยที่ไม่รู้ตัว ไม่ว่ากับดักนั้นจะถูกสร้างมาอย่างตั้งใจหรือไม่ตั้งใจก็ตาม (บางทีอาจเป็นคุณเองนั่นแหละที่เป็นคนวางกับดักตัวเอง…) ในบทความนี้คุณจะได้เรียนรู้อาการแปลกๆ หลายอย่างพร้อมทั้งวิธีแก้ไขด้วยอย่างแน่นอนครับ
ปล. จริงๆ แล้วผมลังเลอยู่นานว่าจะเขียนบทความนี้ออกมาดีมั้ยเพราะอาจมีคนเกรียนๆ เอาวิธีสร้างกับดักเหล่านี้ใช้ทำอะไรแผลงๆ แต่คิดไปคิดมา มันก็เป็นอีกวิธีที่ทำให้ผู้อ่านได้ความรู้ Excel เพิ่มขึ้นได้เช่นกันเลยคิดว่าเขียนดีกว่า
เอาล่ะ เพื่อไม่ให้เสียเวลา มาดูกันเลยดีกว่าว่ามีกับดักอะไรบ้าง?
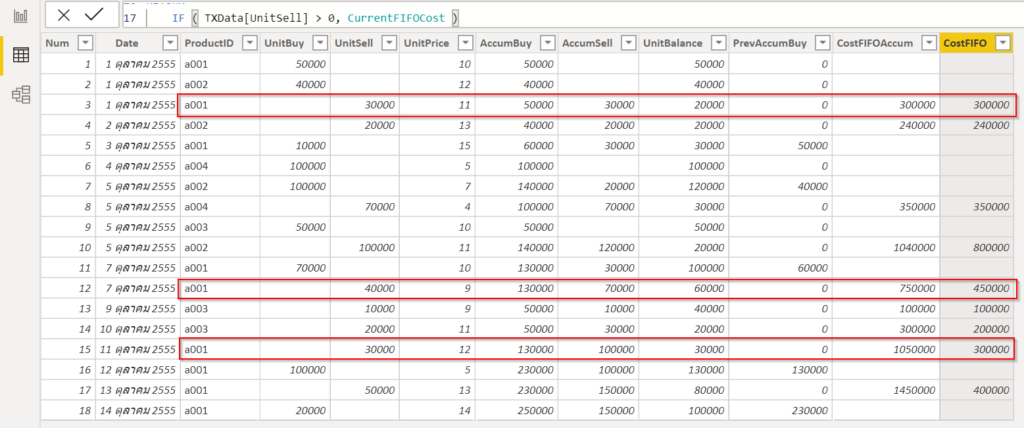
กับดัก 1 : ทำให้เพื่อนเขียนสูตรไม่ติด
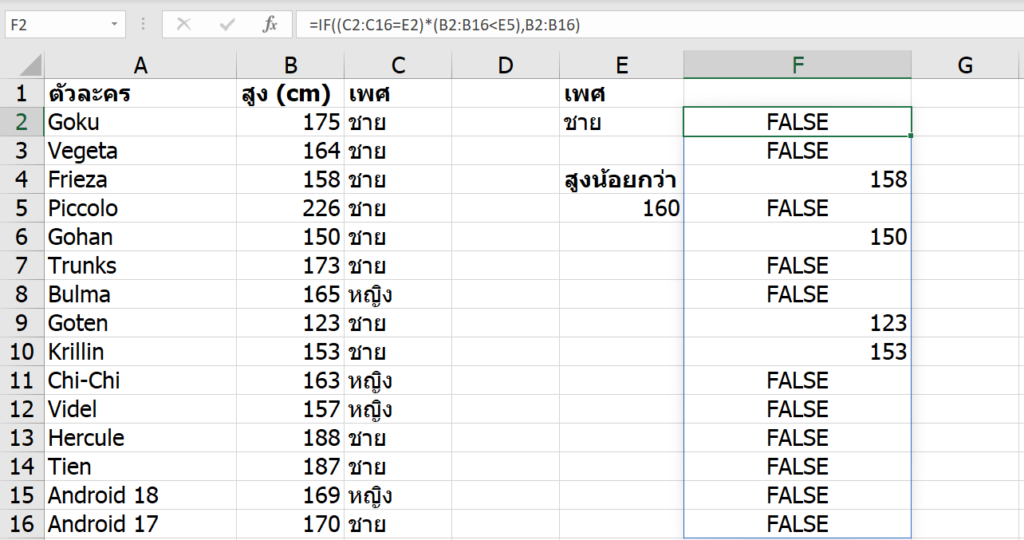
ปกติแล้วเราสามารถปรับ Number Format ให้แต่ละ Cell สามารถแสดงข้อมูลออกมาในรูปแบบที่แตกต่างกันได้ เช่น จะมีทศนิยมกี่ตำแหน่ง จะแสดงเป็น % หรือไม่ ซึ่งหนึ่งในรูปแบบมาตรฐานที่สามารถนำมาแกล้งเพื่อนได้คือ รูปแบบ Text
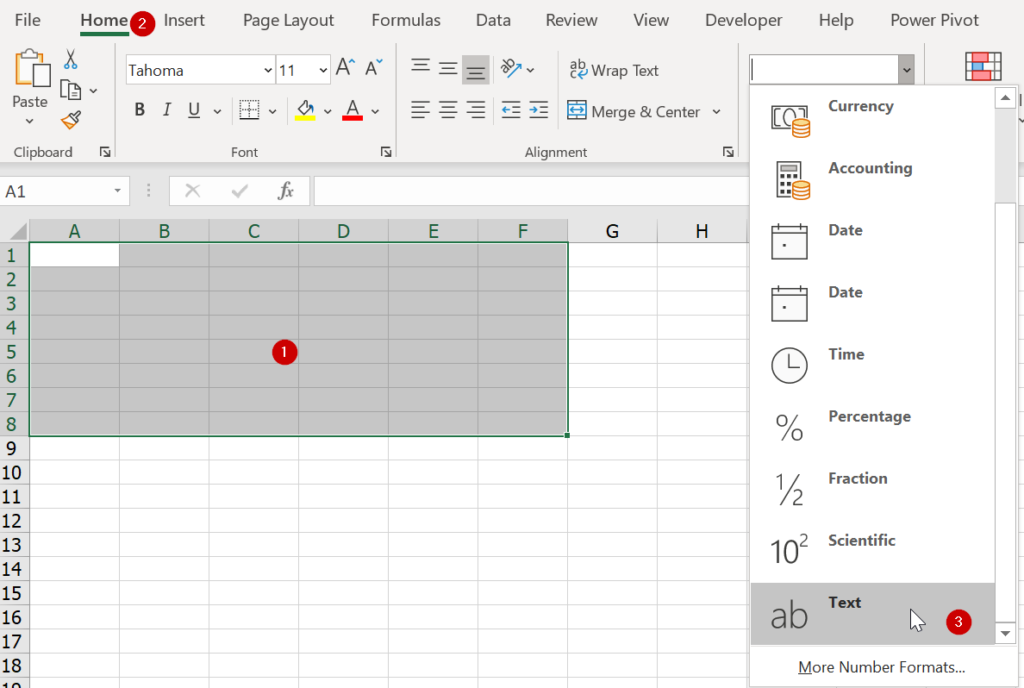
ซึ่งหลังจากปรับ Format เป็น Text แล้วจะทำให้เมื่อพิมพ์อะไรลงไปใน Cell ก็ตาม Excel จะมองว่าข้อมูลนั้นเป็น Text ทั้งหมดเลย โดยไม่ต้องใส่เครื่องหมาย ‘ นำหน้าด้วยซ้ำ (แต่ต้องปรับเป็น Text ก่อนพิมพ์นะ)
ซึ่งการทำให้เป็น Text นั้น Excel ก็จะมองว่าการเขียนสูตร ก็จะกลายเป็น Text ธรรมดาๆ ไปด้วย ทำให้เขียนสูตรไม่ติดนั่นเอง
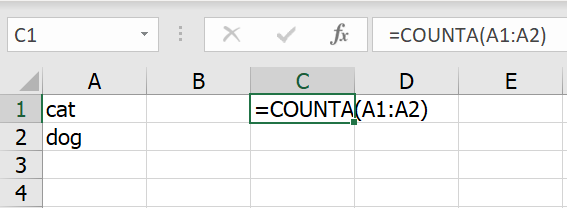
วิธีแก้ไข
ต้องปรับ Format ให้กลับมาเป็น General หรือ Clear Format ทิ้งก็ได้ จากนั้นให้กระตุ้นให้มันคิดว่ามีการพิมพ์ข้อมูลใหม่ ซึ่งเราจะสามารถกระตุ้นให้สูตรกลับมาทำงานอีกครั้งได้ด้วยการ Replace (Ctrl+H) โดยแทนเครื่องหมาย = ด้วย = นั่นเอง
พอแก้ไขแล้วสูตรก็จะกลับมาทำงานอีกครั้งนึง

กับดัก 2 : ทำให้สูตรไม่อัปเดทด้วย Manual Calculation
วิธีนี้เป็นวิธีที่โคตรเลวร้าย เพราะขณะที่เพื่อนเขียนสูตร สูตรมันจะทำงานอยู่ แต่ว่าถ้า input เปลี่ยนไป แทนที่ผลลัพธ์ของสูตรจะอัปเดท มันกลับไม่อัปเดท
วิธีทำคือให้เลือก Formula -> Calculation Options ->Manual
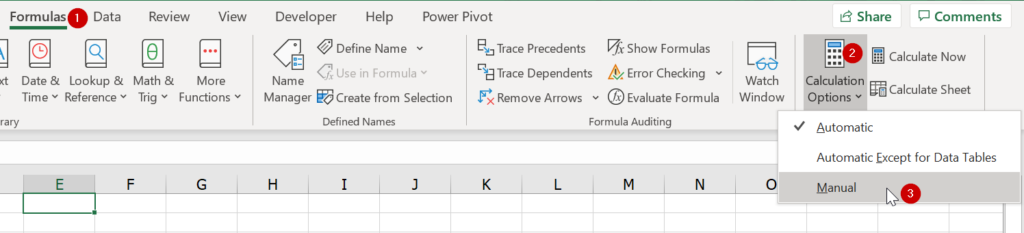
ทีนี้ตอนเขียนสูตรตอนแรกมันจะทำงานได้

แต่พอไปแก้ input ต้นทาง ผลลัพธ์ของสูตรจะไม่อัปเดท
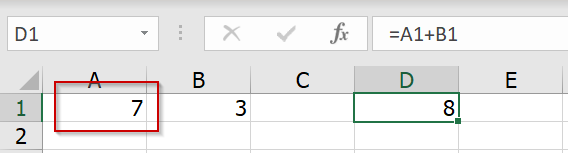
วิธีสังเกตคือ Status Var ด้านซ้ายจะมีคำว่า Calculate ค้างอยู่ แปลว่ามันยังไม่ได้คำนวณอะไรบางอย่าง
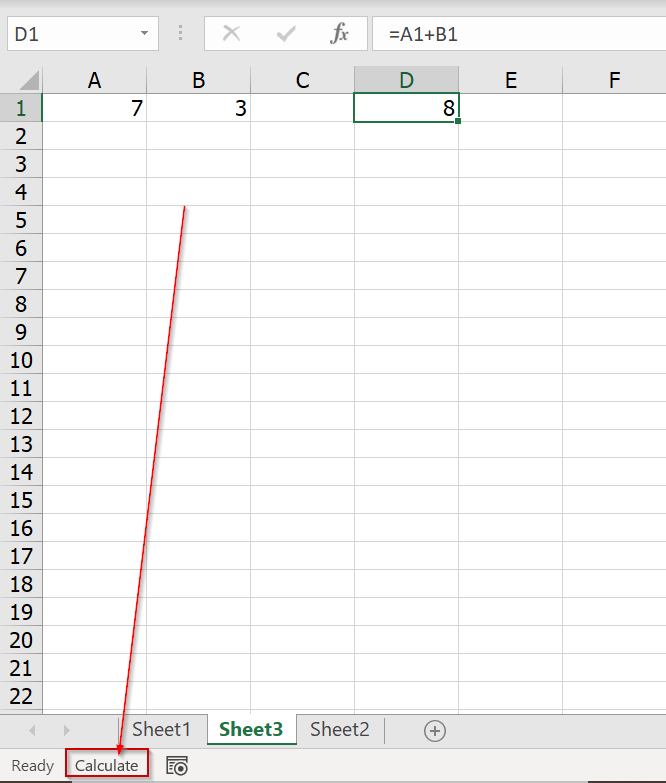
ทดสอบได้ว่า ถ้าลองกดปุ่ม F9 เพื่อบังคับให้มันคำนวณใหม่ คำว่า Calculate จะหายไป และผลลัพธ์การคำนวณจะถูกต้อง
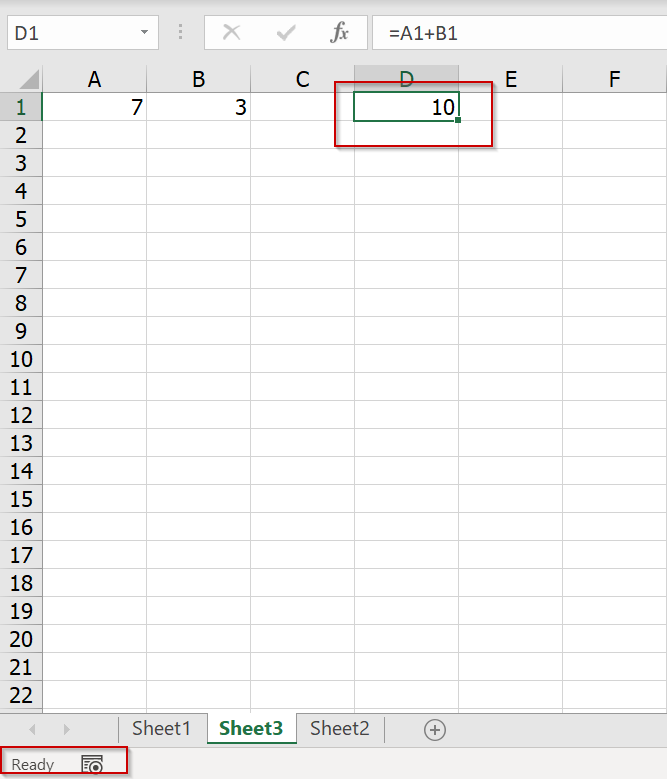
ความเลวร้ายของมันไม่ได้มีแค่นี้ เพราะถ้าเรา Save ไฟล์ที่ปรับแบบ Manual Calculation เอาไว้ แล้วเอาไปให้คนอื่นเปิด เพื่อนของเราก็จะติดอาการ Manual Calculate จากไฟล์นี้ไปด้วยเช่นกัน !
วิธีแก้ไข
ก็ให้ไปเลือก Calculation Options ให้เป็น Automatic ซะก็จบแล้ว
กับดัก 3 : ทำให้มองไม่เห็นข้อมูลด้วยการถม Font สีเดียวกับพื้นหลัง
วิธีแกล้งเพื่อนแบบง่ายๆ อีกอันก็คือ เราไปเปลี่ยน Font ของสีตัวอักษรให้มีสีเดียวกับ Background ซะเลย (ซึ่งมักจะเป็นสีขาว) เพียงเท่านี้เพื่อนก็จะมองไม่เห็นข้อความทีมีอยู่แล้วล่ะ เกรียนแบบทำง่ายมากๆ เลยอันนี้
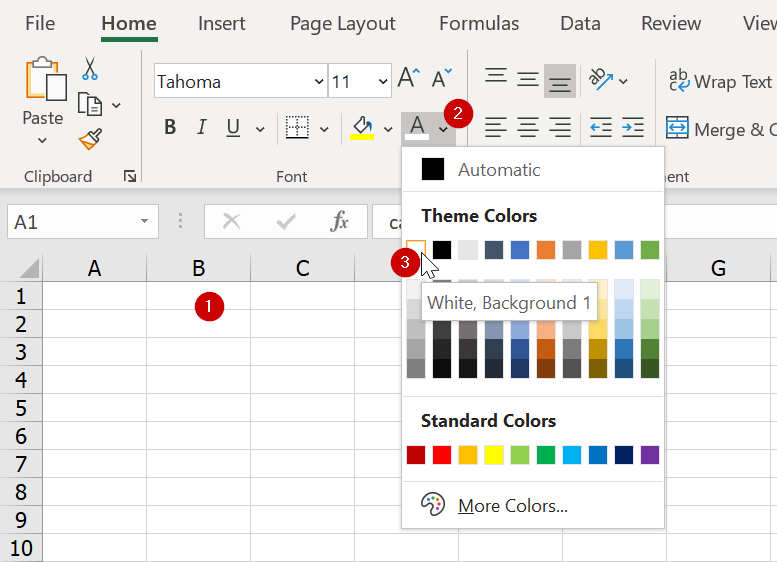
วิธีแก้ไข
การสร้างกับดักอันนี้ง่ายมาก วิธีแก้ไขก็ง่ายมากเช่นกัน แค่เปลี่ยนสี Font เป็นสีอื่น เช่น Automatic หรือสีดำก็หายแล้ว
กับดัก 4 : ทำให้มองไม่เห็นข้อมูลด้วย Custom Number Format
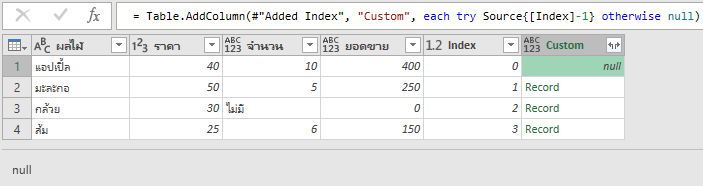
ถ้าใครคิดว่าการใส่ Font สีขาวมัน Basic เกินไป มาดูการแกล้งด้วย Number Format แบบ Advance โดยให้เลือกข้อมูลแล้วใส่ Custom Format เป็น code ดังนี้
;;;
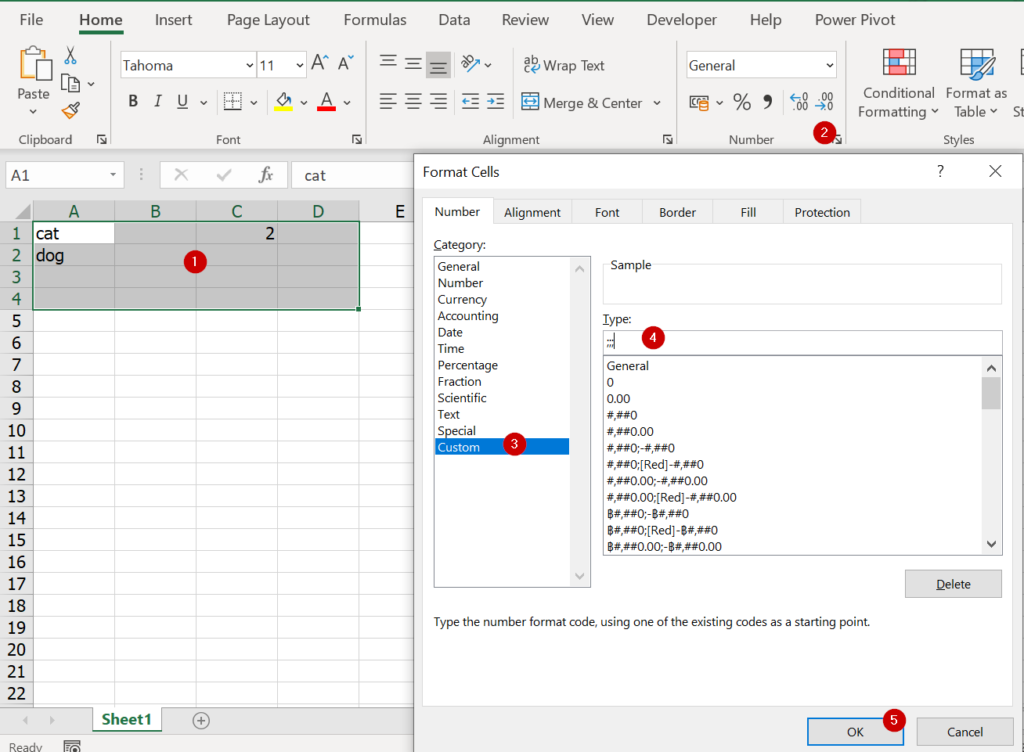
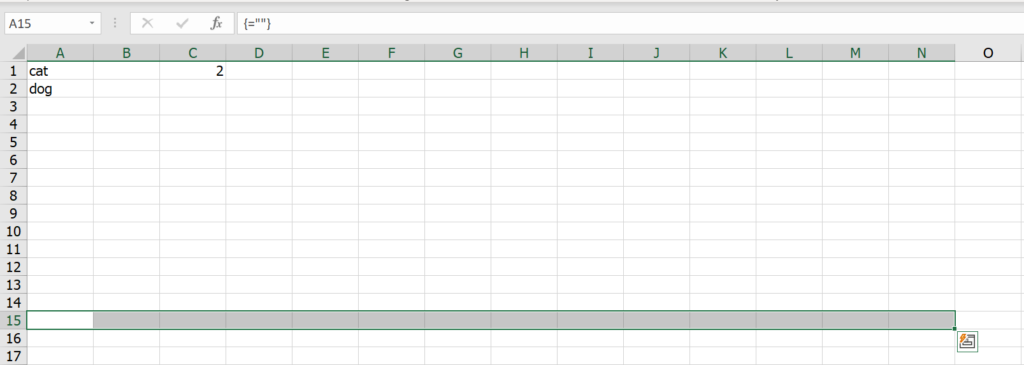
พอกด ok แล้ว ก็จะมองไม่เห็นข้อมูลทันที แต่ข้อมูลไม่ได้หายไปจริงๆนะ แค่มองไม่เห็นเฉยๆ สังเกตได้จากรูปข้างล่าง ตรง Formula Bar ยังมีคำว่า cat อยู่เลย แต่เรามองไม่เห็น

การที่ Custom Format นี้ทำให้ข้อมูลหายไปได้เป็นเพราะว่า Custom Format แบบเต็มยศสามารถระบุได้ดังนี้
Formatเลขบวก ; Formatเลขลบ ; Formatเลขศูนย์ ; Formatตัวหนังสือ
แต่เราใส่แต่ ; ซึ่งเป็นตัวคั่นอย่างเดียว โดยไม่ใส่ code รูปแบบอะไรเลย ทำให้มองไม่เห็นข้อมูลเลยนั่นเองครับ
ใครสงสัยเรื่อง Custom Number Format สามารถไปอ่านรายละเอียดได้ที่นี่เลย
วิธีแก้ไข
วิธีแก้ก็ให้ปรับ Format เป็น General หรือ Clear Format ทิ้งเช่นเดิมครับ
กับดัก 5 : ถมดำพื้นหลังด้วย Conditional Format
ปกติแล้วเครื่องมือ Conditional Format จะสามารถกำหนดได้ว่า หากข้อมูลใน Cell ตรงกับเงื่อนไขที่กำหนด ให้ใส่ Format ตามต้องการได้
ถ้าจะแกล้งเพื่อนเราสามารถเลือกข้อมูลแล้วใส่เงื่อนไขประหลาดๆ เข้าไป เพื่อให้มันถมสีดำทั้ง Font และ Background แค่นี้ใครเจอก็เซ็งแล้วล่ะ เช่น ให้เลือก Highlight Cell Rules แบบ Greater Than
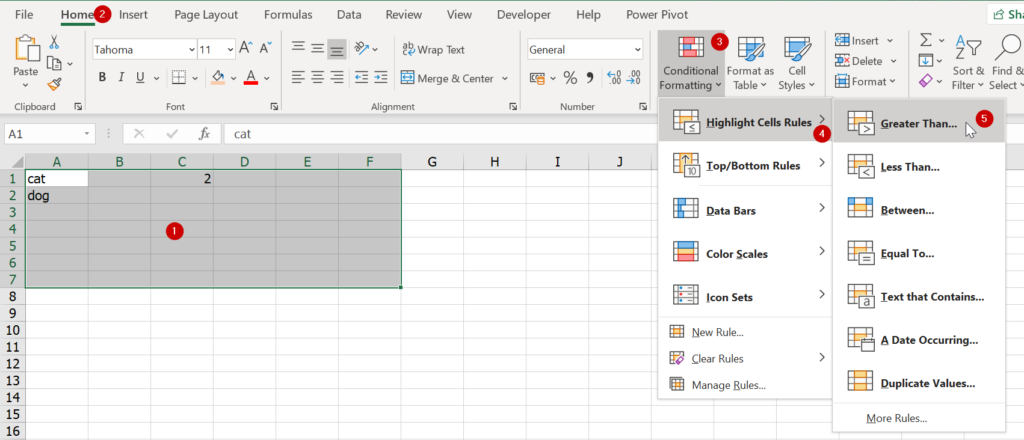
จากนั้นใส่เลขติดลบเยอะๆ ไปเลย เช่น -1000000 แล้วเลือก Custom Format Fill สีดำซะ (สาเหตุที่ใส่เลขติดลบแล้วมันใช้งานได้ เพราะว่า Excel จะมองว่าข้อความจะมีค่ามากกว่าตัวเลขและตัวเลขปกติเราจะไม่ใส่ติดลบ แถมช่องว่าง Excel ก็จะมองว่าเป็นเลข 0 อีก มันจึงตรงเงื่อนไขหมดเลย)

แค่นี้ฉากหลังจะหลายเป็นสีดำทันที แล้วถมสีแก้ไม่ได้ด้วย (เช่นในรูปผมกดถมสีเหลืองแล้ว มันก็ไม่เหลือง)
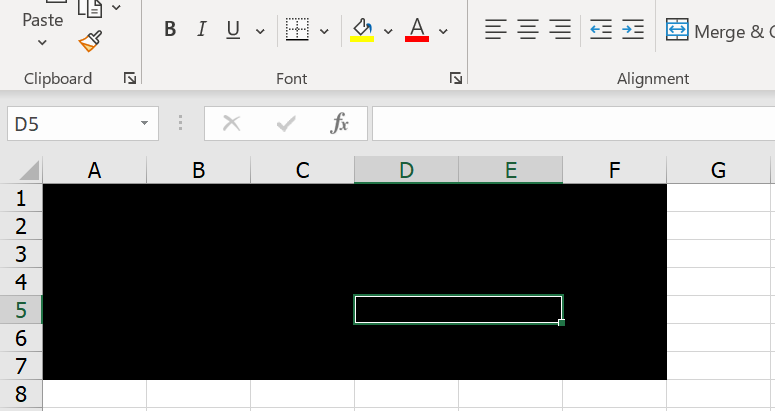
วิธีแก้ไข
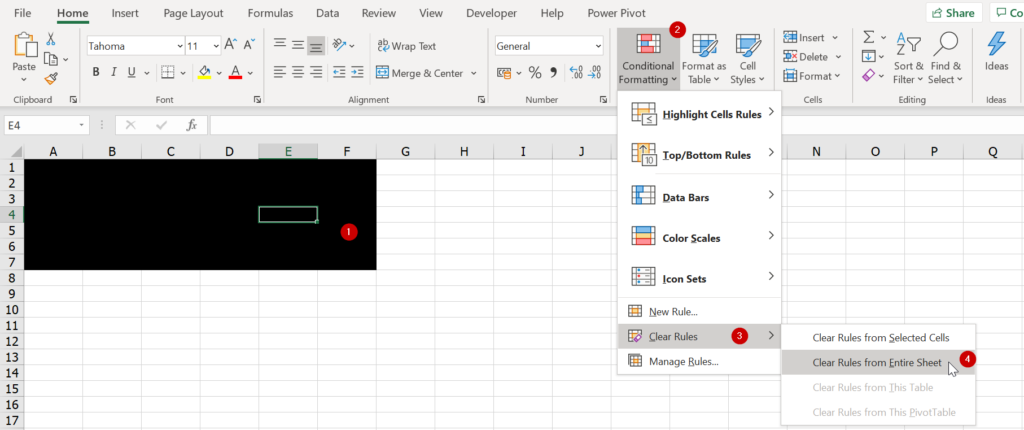
ต้องเอา Conditional Format ออก ซึ่งเราอาจจะลบออกเฉพาะ Cell ที่เลือก หรือจะเอาออกทั้ง Sheet เลยก็ย่อมได้ (แต่ถ้าจะเลือกแบบละเอียด ให้ไปที่ Manage Rules แทน)
กับดัก 6 : ซ่อนคอลัมน์แรกๆ ให้หายไปซะ
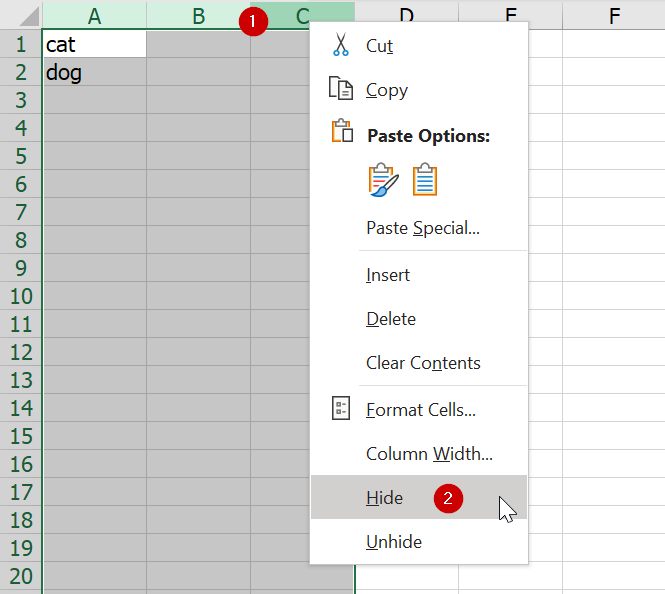
อันนี้จริงๆ เป็นวิธีแกล้งที่เห็นง่าย แก้ง่าย แต่หลายคนแก้ไม่เป็น เช่น หากเราเลือกคอลัมน์แรกๆ แล้วคลิ๊กขวา Hide ซะ แค่นี้คอลัมน์ก็จะถูกซ่อนไป
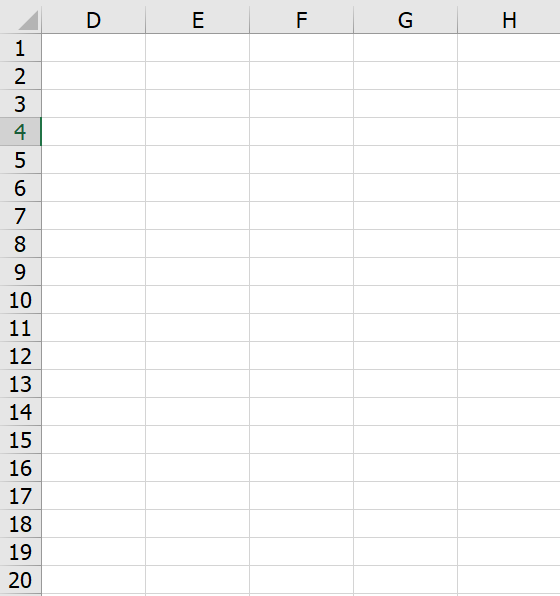
เนี่ย หายไปละ…
วิธีแก้ไข
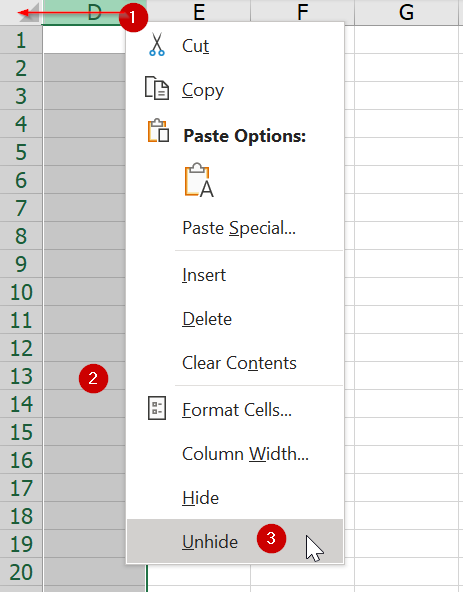
เราจะเลือกคอลัมน์ที่มองเห็นอยู่ตามปกติแล้ว Unhide ธรรมดาๆ ไม่ได้ วิธีที่ถูกต้องคือ ต้องเลือกคอลัมน์แรกที่ยังมองเห็นอยู่แล้วลากไปทางซ้าย แล้วค่อนกดคลิ๊กขวา Unhide จึงจะได้
กับดัก 7 : ทำให้เลื่อน Scroll หน้าจอไม่ได้ด้วยการ Freeze Pane
ปกติแล้วเราจะสามารถ Lock หน้าจอบางส่วนให้ตรึงอยู่กับที่ แม้ว่าจะกด Scroll หน้าจอลงไปข้างล่างหรือไปทางขวาได้ วิธีการทำคือให้เลือกช่องแรกที่จะไม่ Lock แล้วกด View-> Freeze Pane
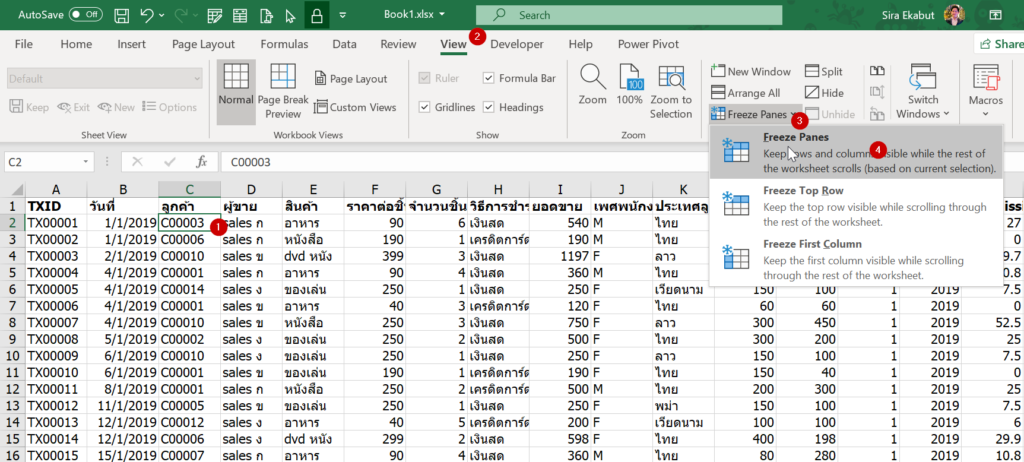
จะพบว่าคอลัมน์ทางซ้าย และแถวข้างบนของ cell ที่เราเลือก (คอลัมน์ A-B และ Row 1) จะถูก Lock ให้อยู่กับที่ไว้ เมื่อทำการเลื่อนหน้าจอไปมา นี่คือการ Freeze Pane ที่ถูกต้อง
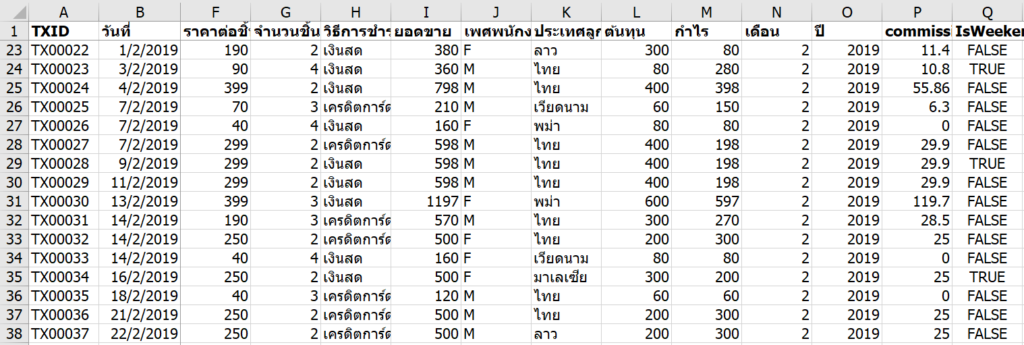
แต่จะเกิดอะไรขึ้น ถ้าเราดันไป Freeze Pane ที่ Cell ขวาล่างมากๆ จนเกือบจะล้นหน้าจอ เช่น R22
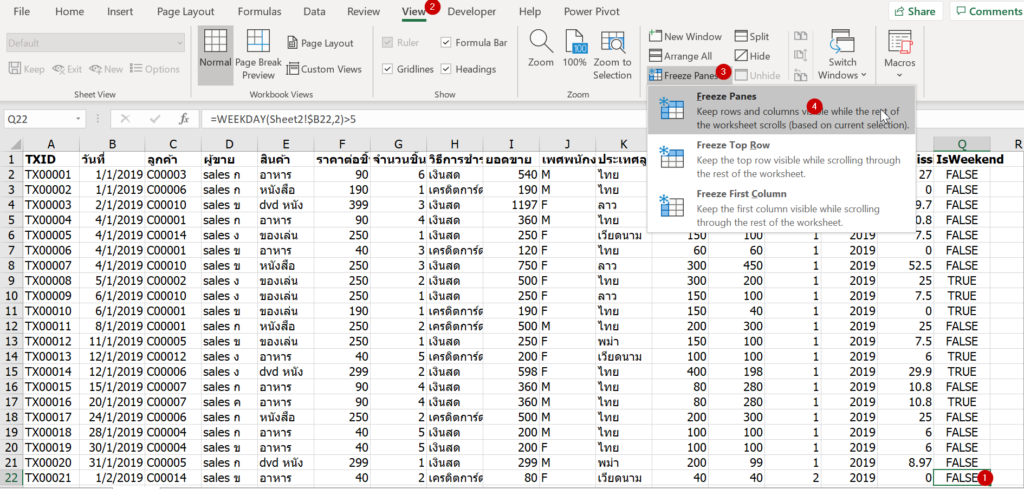
เพื่อนจะเลื่อนหน้าจอแทบไม่ไปเลย งงแน่นอน เกรียนสุดๆ
กับดัก 8 : เปลี่ยน Format วันที่และเวลาให้เป็น General
Excel นั้นมองวันที่และเวลาเป็นแค่ตัวเลขธรรมดาๆ ตัวนึง ดังนั้นหากเราเลือกข้อมูลที่เป็นวันที่ แล้วลองไปเปลี่ยน Number Format ให้เป็น General ดู พวกวันที่จะกลายเป็นเลข 4 หมื่นกว่าๆ ส่วนเวลาจะกลายเป็นทศนิยมไปเลย ดูแล้วปวดหัวมากมาย
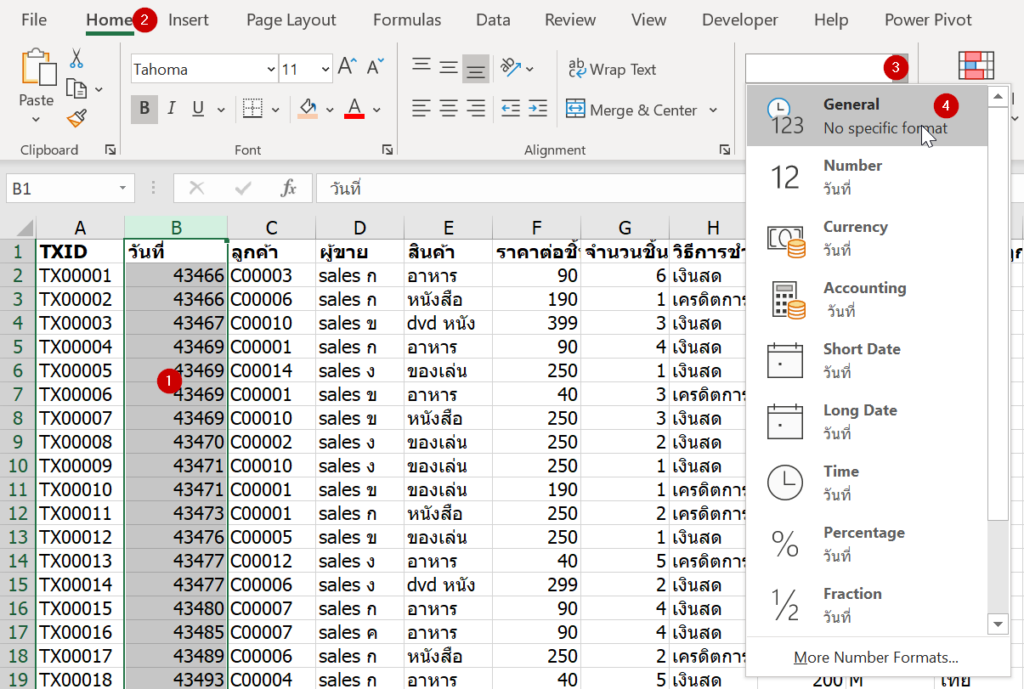
วิธีแก้ไข
แค่เลือก Number Format กลับมาให้เป็นวันที่ก็จบแล้วครับ
กับดัก 9 : เปลี่ยนความกว้างคอลัมน์ให้เหลือนิดเดียว
สำหรับการแกล้งอันนี้เราจะมาเปลี่ยนความกว้างคอลัมน์ให้เหลือน้อยๆ กันครับ เพราะว่าเวลาที่ Excel มีพื้นที่แสดงข้อมูลไม่พอที่จะแสดงตัวเลขหรือวันที่ มันจะขึ้นเครื่องหมาย ### ขึ้นมา ทำให้หลายคนงงได้เลยล่ะ
เราสามารถเปลี่ยนความกว้างคอลัมน์พร้อมกันหลายๆ คอลัมน์ได้เลย โดยเลือกหลายๆ คอลัมน์แล้วลากเปลี่ยนความกว้างทีเดียว
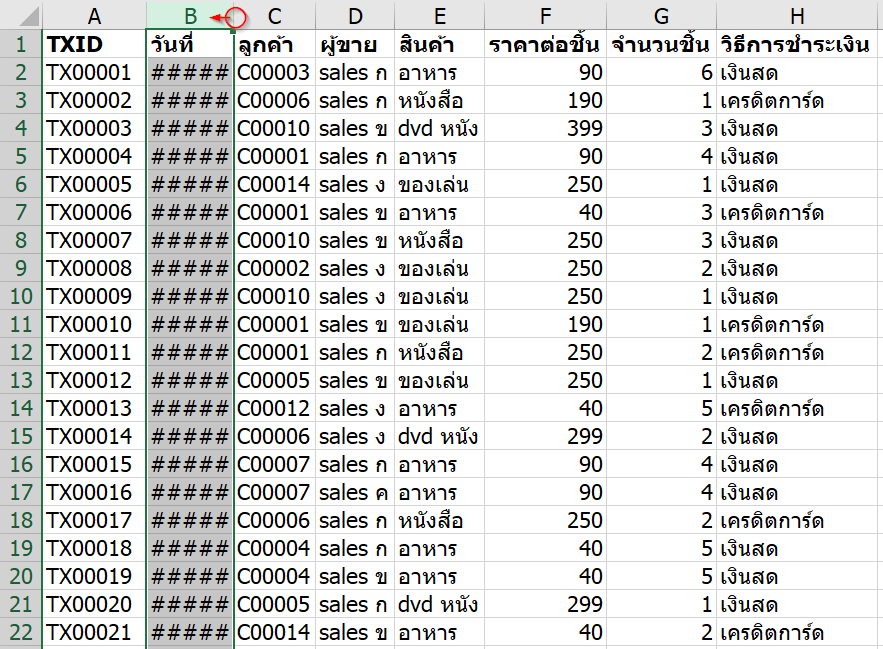
วิธีแก้ไข
วิธีแก้ไขก็ง่ายมาก แค่ปรับความกว้างคอลัมน์ให้เพียงพอก็จบแล้วครับ อาจใช้การดับเบิ้ลคลิ๊กที่ช่องแบ่งคอลัมน์ก็ได้
กับดัก 10 : ทำให้พิมพ์อะไรไม่ได้เลยด้วย Data Validation
ปติแล้วเครื่องมือ Data Validation จะสามารถช่วยให้เราสามารถกำหนดได้ว่าแต่ละ Cell จะยอมให้พิมพ์ข้อมูลแบบไหนลงไปได้บ้าง ซึ่งถ้าพิมพ์ผิดมันจะไม่ยอม
วิธีแกล้งเพื่อน เราก็แค่เลือกพื้นที่แล้วใส่ Data Validation ที่เพื่อนไม่มีทางจะกรอกถูก เช่น ให้เลือกเป็น List แล้วใส่คำแปลกๆ ลงไป แต่ที่สำคัญให้เอา in-cell Dropdown ออก เพื่อนจะได้ไม่รู้ว่าต้องกรอกอะไร

แค่นี้เพื่อนก็จะกรอกอะไรไม่ได้เลย
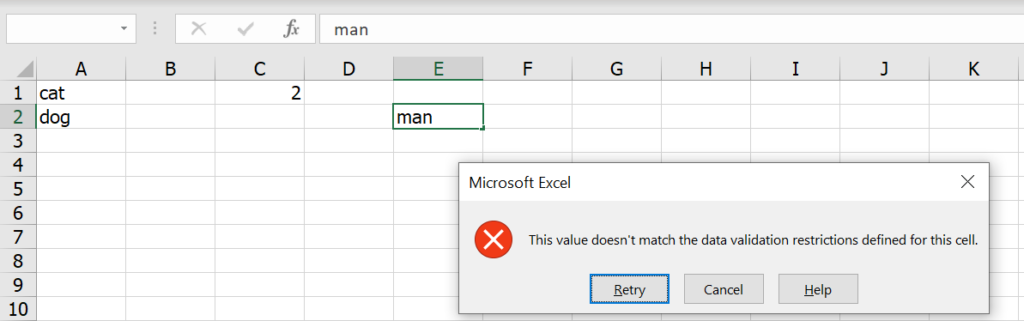
วิธีแก้ไข
แค่เลือกพื้นที่แล้วเลือก Data Validation แบบ Any Value (กรอกอะไรก็ได้) ก็จบเลยครับ
กับดัก 11 : Protect Sheet แบบไม่ต้องใส่ Password
วิธีอันนี้จะทำให้พิมพ์ข้อมูลไม่ได้ในช่องที่ทำการ Lock เอาไว้ ซึ่งตามปกติแล้วทุก Cell ใน Excel จะถูก Lockไว้ตั้งแต่ต้นอยู่แล้ว ดังนั้นเมื่อไหร่ที่ทำการ Activate การ Protect Sheet ขึ้นมาจริงๆ เราจะไม่สามารถแก้ไขอะไรใน Cell ได้เลย
ดังนั้นวิธีการทำกับดัก ก็แค่ไปที่ Review -> Protect Sheet -> ok จบเลย
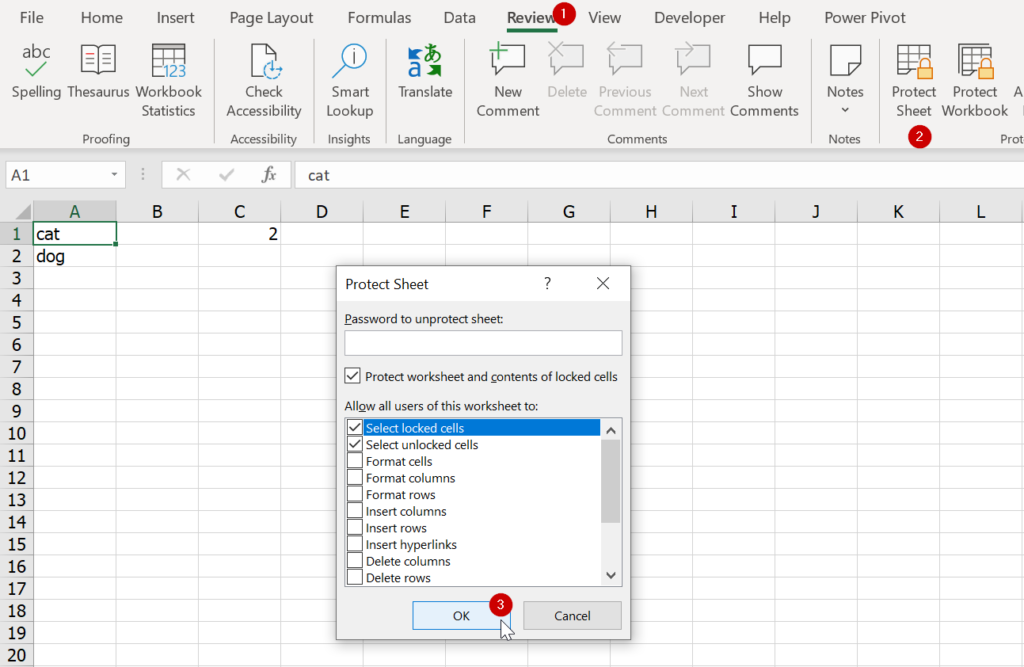
แค่นี้เพื่อนก็จะไม่สามารถพิมพ์หรือแก้อะไรได้เลย
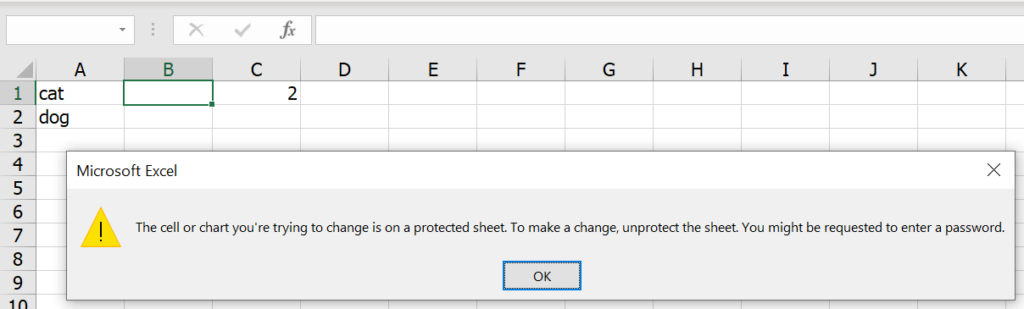
วิธีแก้ไข
แค่ไปที่ Review -> Unprotect Sheet ก็หายเลยครับ
Tips : การ Protect sheet ในชีวิตจริง เราจะต้องมาเลือกบาง cell ที่ยอมให้เพื่อนกรอกได้ แล้วเอาการ Lock Cell ออกซะ ก่อนที่จะทำการ Protect Sheet จริงๆ
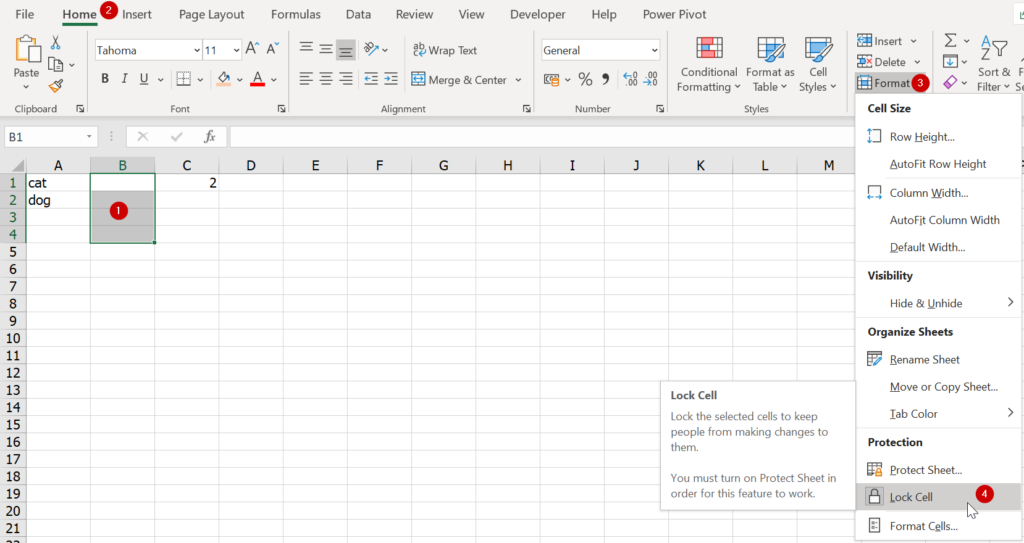
กับดัก 12 : ทำให้แทรกคอลัมน์ แทรกแถวไม่ได้ด้วย Array Formula
การเขียนสูตรแบบ Array Formula นั้น หากเราเขียนสูตรให้ผลลัพธ์แสดงออกมาหลายช่อง เวลาจะแก้ไขจะไม่สามารถแก้ช่องใดช่องหนึ่งได้ จะต้องแก้ไขโดยเลือกทั้ง Array แล้วแก้ไขเท่านั้น
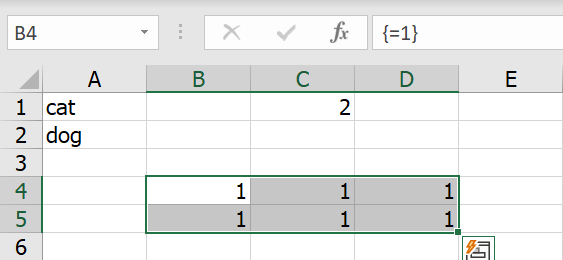
เช่น หากเราลองเลือกพื้นที่แล้วใส่สูตรว่า =1 แล้วกด Ctrl+Shift+Enter เพื่อเรียกใช้สูตรแบบ Array

พอกด Ctrl+Shift+Enter แล้วจะมีเครื่องหมายปีกกามาครอบสูตรของเราเอง
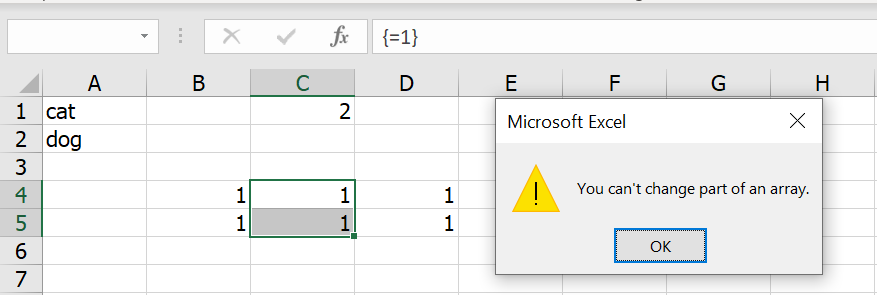
ซึ่งหากเราลองเลือกแค่บางส่วนของสูตร Array แล้วกด ปุ่ม del บน Keyboard เพื่อลบข้อมูล มันจะไม่ยอม โดยจะบอกว่าเราไม่สามารถแก้ไขบางส่วนของ Array ได้
ซึ่งก็จะไม่สามารถแทรกแถว หรือ ลบแถว หรือคอลัมน์ เช่นกัน ยกเว้นว่าจะเลือกข้อมูลสูตร Array ทั้งหมดก่อนแล้วกดปุ่ม del บน Keyboard จึงจะลบได้
ความเลวร้ายคือ หากเราใส่สูตรว่า =”” แล้วกด Ctrl+Shift+Enter เพื่อนจะมองไม่เห็นผลลัพธ์เพราะมันเป็น Array ของ Blank Text
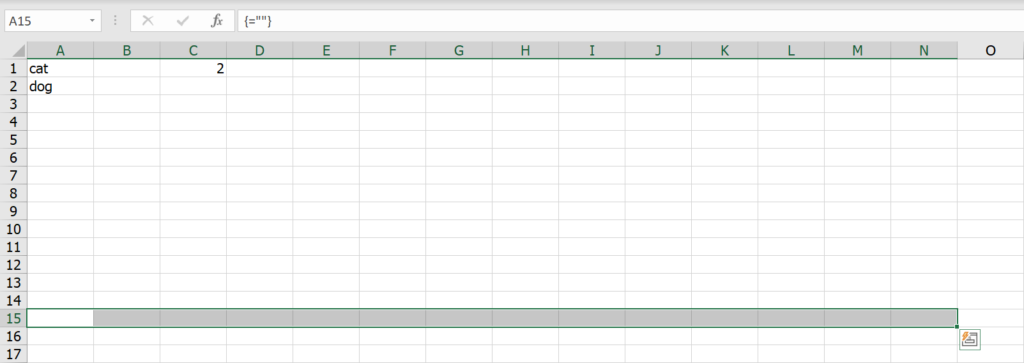
เพื่อนจะงงทันทีว่าทำไมเค้าถึงแทรกคอลัมน์ไม่ได้!
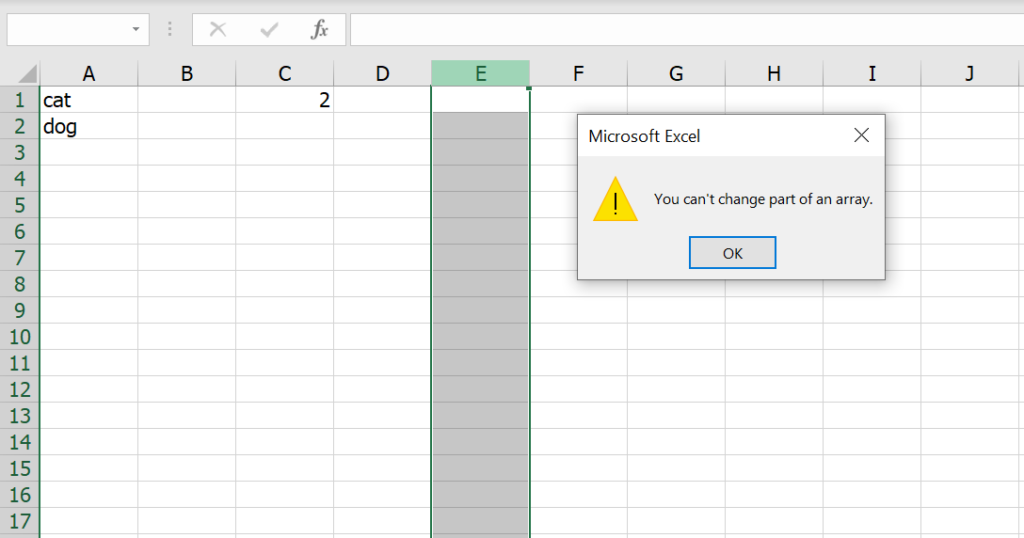
วิธีแก้ไข
ให้หา Array ว่างเปล่านั้นให้เจอแล้วลบทิ้งซะ ซึ่งการหา Array ให้เจอมันมีเทคนิคอยู่คือ ให้เลือกทั้งคอลัมน์(ที่เราลองแทรกแล้วไม่ได้) แล้วให้ใช้ Go to Special (Ctrl+g) –> Special ในการหาช่องที่เป็นสูตรก่อน
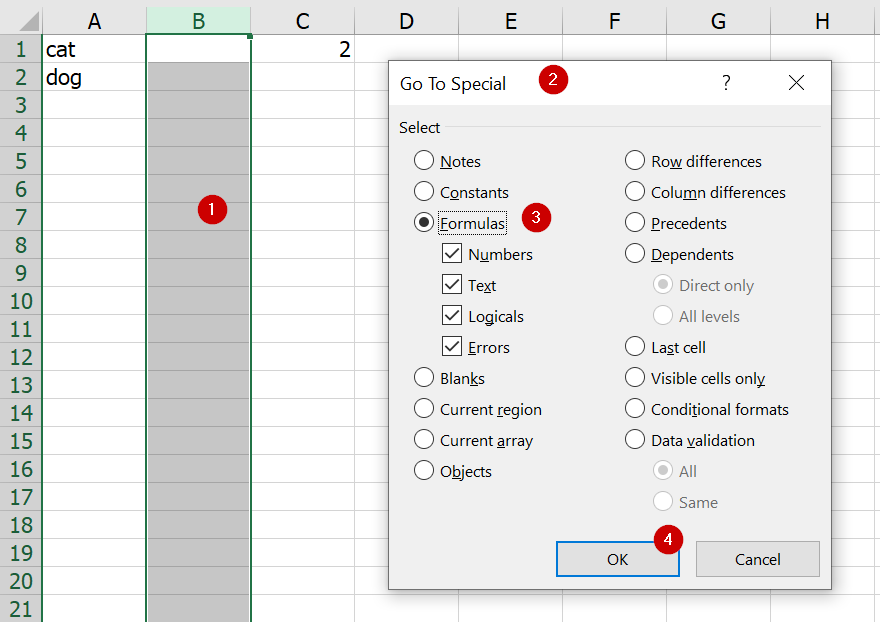
มันจะเด้งมาเลือกช่องนึงที่มีสูตร Array อยู่
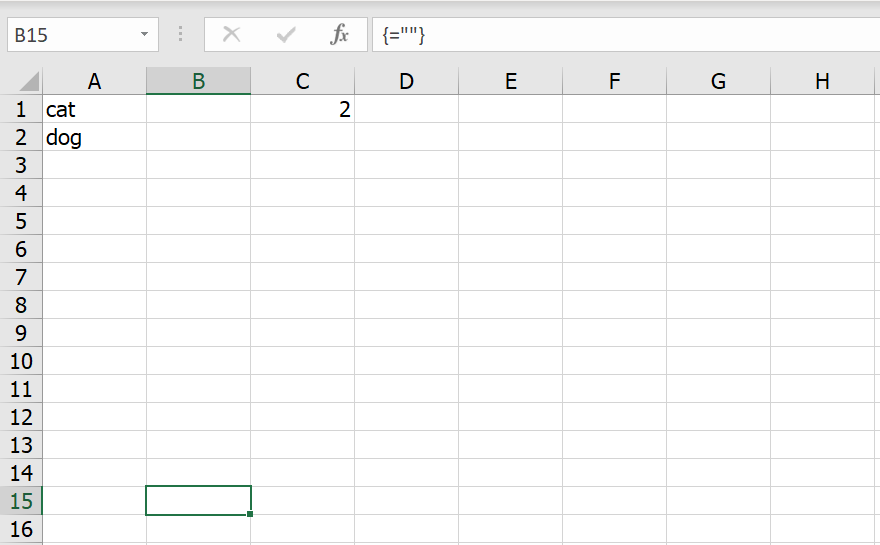
ให้เรา Go to Special อีกทีแล้วเลือก Current Array (หรือกด Ctrl+/) มันจะเลือกพื้นที่ Array นั้นทั้งหมดให้เลย
คราวนี้เราก็สามารถกดปุ่ม del บน Keyboard เพื่อลบ Array นั้นทิ้งได้แล้ว
กับดัก 13 : ซ่อน Sheet แบบ Very Hidden
ปกติแล้วเราจะสามารถซ่อน Sheet ใดๆ ที่ต้องการได้โดยกดคลิ๊กขวาที่ tab sheet แล้วเลือก Hide เพื่อซ่อน sheet ที่ต้องการได้เลย แต่วิธีนี้มันก็สามารถ Unhide ได้ง่ายๆ โดยกดคลิ๊กขวา Unhide ได้เลย
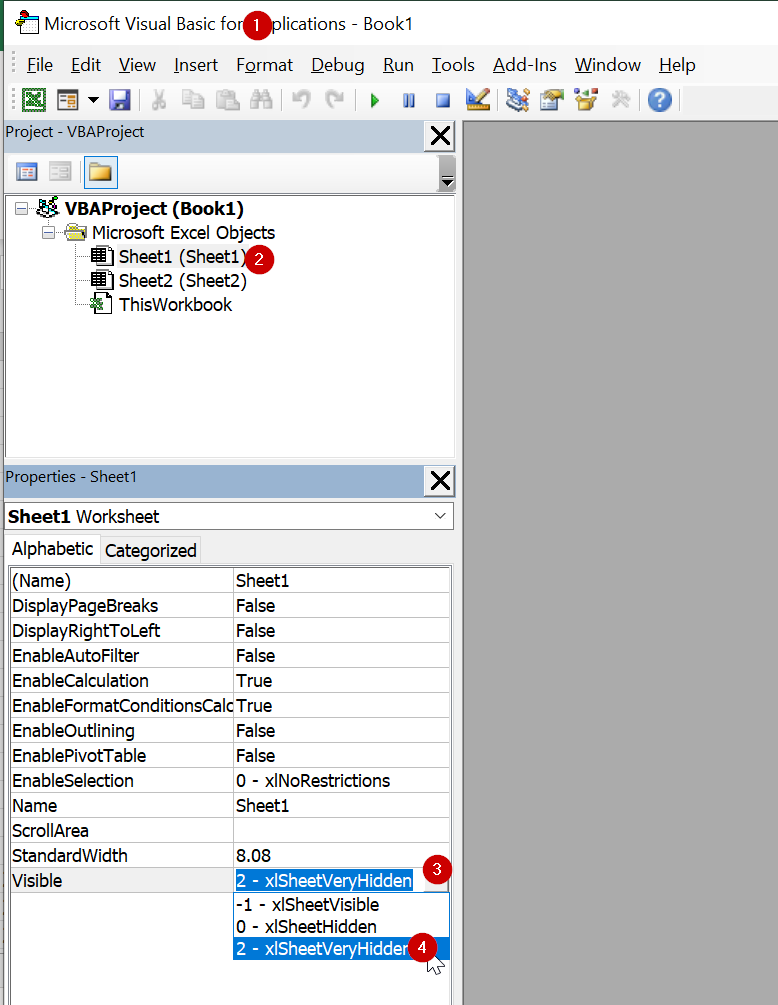
วิธีที่แสบกว่าคือ กด Alt+F11 เพื่อเปิด Visual Basic Editor แล้วซ่อน Sheet แบบ Very Hidden ซะ ดังนี้
จากนั้นก็กดปิดเจ้า Visual Basic Editor ซะ
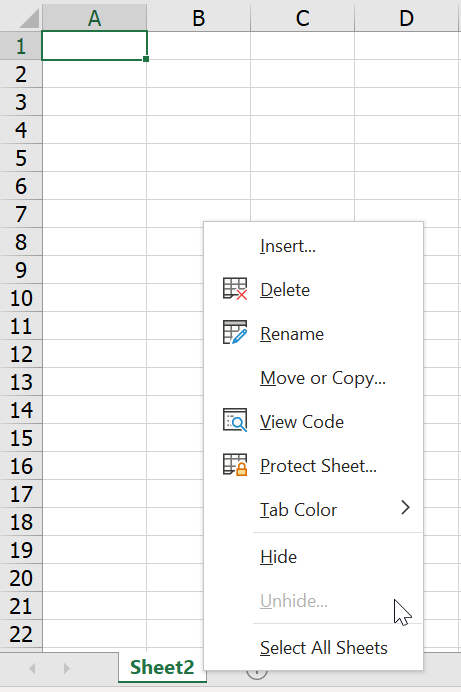
พอเราคลิ๊กขวาที่ sheet จะพบว่ามันไม่มีอะไรให้ Unhide แล้ว และเพื่อนก็งงทันที!
วิธีแก้ไข
วิธีแก้ก็ต้องกด Alt+F11 เข้าไปยัง Visual Basic Editor แล้วแก้กลับมาเป็น Visible เหมือนเดิม

จบแล้ว
จริงๆ กับดักเกรียนๆ ยังมีอีกเยอะแยะเลย แต่ใครโดนกับดักแบบในบทความนี้ไปมีปวดหัวแน่นอน (แค่นี้เพื่อนก็จะเลิกคบแล้วล่ะ) พอดีกว่าเนอะ แต่ถ้าใครมีไอเดียเกรียนๆ จะแบ่งปันก็บอกมาได้นะครับ